TIP4P/2005 model of water: Difference between revisions
m (→References: Tidied reference.) |
Carl McBride (talk | contribs) (→References: Added a recent publication) |
||
| (34 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
The '''TIP4P/2005''' model | The '''TIP4P/2005''' model | ||
TIP4P/2005 is a rigid planar model, having a similar geometry to the Bernal and Fowler | <ref>[http://dx.doi.org/10.1063/1.2121687 J. L. F. Abascal and C. Vega "A general purpose model for the condensed phases of water: TIP4P/2005", Journal of Chemical Physics, '''123''' 234505 (2005)]</ref> | ||
is a re-parameterisation of the original [[TIP4P]] potential for [[Computer simulation techniques | simulations]] of [[water]]. | |||
TIP4P/2005 is a rigid planar model, having a similar geometry to that of the [[BF |Bernal and Fowler model]]. | |||
==Parameters== | ==Parameters== | ||
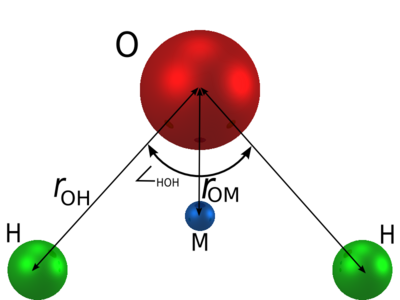
[[Image: | The TIP4P/2005 model consists of a [[Lennard-Jones model | Lennard-Jones site]] for the [[oxygen]] atom, and three charge sites. | ||
::[[Image:Four_site_water_model.png|400px]] | |||
{| style="width: | |||
{| style="width:65%; height:100px" border="1" | |||
|- | |- | ||
| <math>r_{\mathrm {OH}}</math> (Å)|| <math>\angle</math>HOH , deg|| <math>\sigma</math> (Å)|| <math>\epsilon/k</math> (K)|| q(O) (e) || q(H) (e) || q(M) (e) || <math>r_{\mathrm {OM}}</math> (Å) | | <math>r_{\mathrm {OH}}</math> (Å)|| <math>\angle</math>HOH , deg|| <math>\sigma</math> (Å)|| <math>\epsilon/k</math> (K)|| q(O) (e) || q(H) (e) || q(M) (e) || <math>r_{\mathrm {OM}}</math> (Å) | ||
| Line 14: | Line 18: | ||
*[[DL_POLY FIELD file for the TIP4P/2005 model]] | *[[DL_POLY FIELD file for the TIP4P/2005 model]] | ||
*[http:// | *[[GROMACS files for the TIP4P/2005 model]] | ||
*[[NAMD]] [http://catalan.quim.ucm.es/namd/tip4p_2005_namd.tar.gz files for the TIP4P/2005 model] | |||
==Phase diagram== | ==Phase diagram== | ||
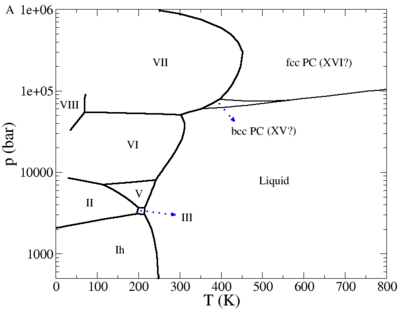
The [[Phase diagrams | phase diagram]] of the TIP4P/2005 model is given in a publication by Abascal, Sanz and Vega | The [[Phase diagrams | phase diagram]] of the TIP4P/2005 model in the [[Phase diagrams: Pressure-temperature plane |pressure-temperature plane]] (adapted from Fig. 9a of <ref name="multiple2">[http://dx.doi.org/10.1063/1.3156856 J. L. Aragones and C. Vega "Plastic crystal phases of simple water models", Journal of Chemical Physics '''130''' 244504 (2009)]</ref>) | ||
is given in a publication by Abascal, Sanz and Vega <ref>[http://dx.doi.org/10.1039/b812832d Jose L. F. Abascal, Eduardo Sanz and Carlos Vega "Triple points and coexistence properties of the dense phases of water calculated using computer simulation", Physical Chemistry Chemical Physics '''11''' pp. 556-562 (2009)]</ref> (revisited by Conde et. al. <ref>[http://dx.doi.org/10.1063/1.4824627 M. M. Conde , M. A. Gonzalez , J. L. F. Abascal and C. Vega "Determining the phase diagram of water from direct coexistence simulations: The phase diagram of the TIP4P/2005 model revisited", Journal of Chemical Physics '''139''' 154505 (2013)]</ref>) | |||
and for negative [[pressure]]s in the publication | |||
<ref>[http://dx.doi.org/10.1063/1.3182727 M. M. Conde, C. Vega, G. A. Tribello, and B. Slater "The phase diagram of water at negative pressures: Virtual ices", Journal of Chemical Physics '''131''' 034510 (2009)]</ref>. | |||
:[[Image:TIP4P_2005_phase_diagram.png|400px]] | |||
====Liquid-vapour equilibria==== | |||
<ref>[http://dx.doi.org/10.1063/1.2215612 C. Vega, J. L. F. Abascal and I. Nezbeda "Vapor-liquid equilibria from the triple point up to the critical point for the new generation of TIP4P-like models: TIP4P/Ew, TIP4P/2005, and TIP4P/ice" Journal of Chemical Physics '''125''' 034503 (2006)]</ref> | |||
====Plastic crystal phases==== | |||
Recent simulations have suggested the possibility of a [[Plastic crystals | plastic crystal]] phase or phases for water <ref name="multiple2"></ref><ref>[http://dx.doi.org/10.1039/b812834k J. L. Aragones, M. M. Conde, E. G. Noya and C. Vega "The phase diagram of water at high pressures as obtained by computer simulations of the TIP4P/2005 model: the appearance of a plastic crystal phase", Physical Chemistry Chemical Physics '''11''' pp. 543- (2009)]</ref> | |||
====Supercooled region==== | |||
The [[Supercooling and nucleation | supercooled]] region has been studied by Abascal and Vega <ref>[http://dx.doi.org/10.1063/1.3585676 J. L. F. Abascal and C. Vega "Note: Equation of state and compressibility of supercooled water: Simulations and experiment", Journal of Chemical Physics '''134''' 186101 (2011)]</ref>, locating a [[Widom line]] <ref>[http://dx.doi.org/10.1063/1.3594545 K. T. Wikfeldt, C. Huang, A. Nilsson, and L. G. M. Pettersson "Enhanced small-angle scattering connected to the Widom line in simulations of supercooled water", Journal of Chemical Physics '''134''' 214506 (2011)]</ref>, indicating a [[second critical point for water]] located at 1350 bar and 193 K. | |||
==Surface tension== | ==Surface tension== | ||
The [[surface tension]] has been studied for the TIP4P/2005 model | The [[surface tension]] has been studied for the TIP4P/2005 model, giving <math>\gamma = 69.1</math> mJ/m<sup>2</sup> at 300 K using the [[test area method]] | ||
<ref>[http://dx.doi.org/10.1063/1.2715577 C. Vega and E. de Miguel "Surface tension of the most popular models of water by using the test-area simulation method", Journal of Chemical Physics '''126''' 154707 (2007)]</ref>, <math>\gamma = 68.4</math> mN/m at 300 K using using the [[Ewald sum]]s for the dispersion interactions | |||
<ref>[http://dx.doi.org/10.1063/1.3279128 José Alejandre and Gustavo A. Chapela "The surface tension of TIP4P/2005 water model using Ewald sums for the dispersion interactions", Journal of Chemical Physics '''132''' 014701 (2010)]</ref>, <math>\gamma = 59</math> mJ/m<sup>2</sup> at 350 K using the [[reaction field]] method | |||
<ref>[http://dx.doi.org/10.1063/1.3422528 J. M. Míguez, D. González-Salgado, J. L. Legido, and M. M. Piñeiro "Calculation of interfacial properties using molecular simulation with the reaction field method: Results for different water models", Journal of Chemical Physics '''132''' 184102 (2010)]</ref> and <math>\gamma = 74.8</math> mN/m at 249 K <ref>[http://dx.doi.org/10.1063/1.3574038 Ryuji Sakamaki, Amadeu K. Sum, Tetsu Narumi, and Kenji Yasuoka "Molecular dynamics simulations of vapor/liquid coexistence using the nonpolarizable water models", Journal of Chemical Physics '''134''' 124708 (2011)]</ref>. | |||
==Self-diffusion coefficient== | ==Self-diffusion coefficient== | ||
The TIP4P/2005 potential has a [[Diffusion |self-diffusion]] coefficient, in bulk water at 298 K, of 0.21 Å<sup>2</sup> ps<sup>−1</sup> in a classical simulation of 216 water molecules (experimental value: 0.23 Å<sup>2</sup> ps<sup>−1</sup>) | The TIP4P/2005 potential has a [[Diffusion |self-diffusion]] coefficient, in bulk water at 298 K, of 0.21 Å<sup>2</sup> ps<sup>−1</sup> in a classical simulation of 216 water molecules (experimental value: 0.23 Å<sup>2</sup> ps<sup>−1</sup>) | ||
<ref>[http://dx.doi.org/10.1063/1.2925792 Thomas E. Markland, Scott Habershon, and David E. Manolopoulos "Quantum diffusion of hydrogen and muonium atoms in liquid water and hexagonal ice", Journal of Chemical Physics '''128''' 194506 (2008)]</ref>. See also <ref>[http://dx.doi.org/10.1063/1.3677196 Dmitri Rozmanov and Peter G. Kusalik "Transport coefficients of the TIP4P-2005 water model", Journal of Chemical Physics '''136''' 044507 (2012)]</ref>. | |||
==Shear viscosity== | |||
The [[shear viscosity]] for the TIP4P/2005 model is 0.855 mPa.s at 298 K and 1 bar <ref>[http://dx.doi.org/10.1063/1.3330544 Miguel Angel González and José L. F. Abascal "The shear viscosity of rigid water models", Journal of Chemical Physics '''132''' 096101 (2010)]</ref> (experimental value 0.896 mPa.s <ref>[http://dx.doi.org/10.1021/je049918m Kenneth R. Harris and Lawrence A. Woolf "Temperature and Volume Dependence of the Viscosity of Water and Heavy Water at Low Temperatures", Journal of Chemical & Engineering Data '''49''' pp. 1064-1069 (2004)]</ref>). | |||
==Liquid-liquid critical point== | |||
For the TIP4P/2005 model the [[Liquid-liquid phase transitions | liquid-liquid]] [[critical points | critical point]] is located at: <math>T_c = 193</math>K, <math>p_c =135</math> MPa and having a density of <math>\rho_c =1012</math> kg/m<sup>3</sup> <ref>[http://dx.doi.org/10.1063/1.3506860 José L. F. Abascal and Carlos Vega "Widom line and the liquid–liquid critical point for the TIP4P/2005 water model", Journal of Chemical Physics '''133''' 234502 (2010)]</ref>. <math>T_c = 182</math>K, <math>p_c =170</math> MPa and having a density of <math>\rho_c =1017</math> kg/m<sup>3</sup> <ref>[http://dx.doi.org/10.1063/1.4944986 Rakesh S. Singh, John W. Biddle, Pablo G. Debenedetti and Mikhail A. Anisimov "Two-state thermodynamics and the possibility of a liquid-liquid phase transition in supercooled TIP4P/2005 water", Journal of Chemical Physics '''144''' 144504 (2016)]</ref>. | |||
==Structure factor== | |||
The [[structure factor]], in particular for small wave vectors, has been calculated by Sedlmeier, Horinek and Netz <ref>[http://dx.doi.org/10.1021/ja1064137 Felix Sedlmeier, Dominik Horinek, and Roland R. Netz "Spatial Correlations of Density and Structural Fluctuations in Liquid Water: A Comparative Simulation Study", Journal of the American Chemical Society Article ASAP (2011)]</ref>, who observe that the TIP4P/2005 model yields an "almost quantitative agreement". | |||
==Virial coefficients== | |||
The [[second virial coefficient]] has been calculated by Chialvo et al <ref>[http://dx.doi.org/10.1016/j.molliq.2006.08.018 Ariel A. Chialvo, Albert Bartók and András Baranyai "On the re-engineered TIP4P water models for the prediction of vapor–liquid equilibrium", Journal of Molecular Liquids '''129''' pp. 120-124 (2006)]</ref>. | |||
==Thermal conductivity== | |||
[[Thermal conductivity]] <ref>[http://dx.doi.org/10.1063/1.4739855 Frank Römer, Anders Lervik, and Fernando Bresme "Nonequilibrium molecular dynamics simulations of the thermal conductivity of water: A systematic investigation of the SPC/E and TIP4P/2005 models", Journal of Chemical Physics '''137''' 074503 (2012)]</ref>. | |||
==Melting point== | |||
<math> T_m = 249.5 \pm 0.1</math> K <ref>[https://doi.org/10.1063/1.5008478 M. M. Conde, M. Rovere, and P. Gallo "High precision determination of the melting points of water TIP4P/2005 and water TIP4P/Ice models by the direct coexistence technique", Journal of Chemical Physics '''147''' 244506 (2017)]</ref>. | |||
==References== | ==References== | ||
<references/> | |||
'''Related reading''' | |||
*[http://dx.doi.org/10.1080/00268970902784926 Helena L. Pi, Juan L. Aragones, Carlos Vega, Eva G. Noya, Jose L. F. Abascal, Miguel A. Gonzalez and Carl McBride "Anomalies in water as obtained from computer simulations of the TIP4P/2005 model: density maxima, and density, isothermal compressibility and heat capacity minima", Molecular Physics '''107''' pp. 365-374 (2009)] | |||
*[http://dx.doi.org/10.1063/1.4960185 Miguel A. González, Chantal Valeriani, Frédéric Caupin and José L. F. Abascal "A comprehensive scenario of the thermodynamic anomalies of water using the TIP4P/2005 model", Journal of Chemical Physics '''145''' 054505 (2016)] | |||
*[https://doi.org/10.1063/1.5023894 Philip H. Handle and Francesco Sciortino "Potential energy landscape of TIP4P/2005 water", Journal of Chemical Physics '''148''' 134505 (2018)] | |||
==External links and resources== | |||
*[http://emoles.quim.ucm.es/pdf/aiche_talk_web.pdf Presentation: Comparing the performance of TIP4P/2005 with other water models] | |||
[[Category: Water]] | [[Category: Water]] | ||
[[Category: Models]] | [[Category: Models]] | ||
{{numeric}} | {{numeric}} | ||
Latest revision as of 14:13, 17 April 2018
The TIP4P/2005 model [1] is a re-parameterisation of the original TIP4P potential for simulations of water. TIP4P/2005 is a rigid planar model, having a similar geometry to that of the Bernal and Fowler model.
Parameters[edit]
The TIP4P/2005 model consists of a Lennard-Jones site for the oxygen atom, and three charge sites.
| (Å) | HOH , deg | (Å) | (K) | q(O) (e) | q(H) (e) | q(M) (e) | (Å) |
| 0.9572 | 104.52 | 3.1589 | 93.2 | 0 | 0.5564 | -2q(H) | 0.1546 |
- DL_POLY FIELD file for the TIP4P/2005 model
- GROMACS files for the TIP4P/2005 model
- NAMD files for the TIP4P/2005 model
Phase diagram[edit]
The phase diagram of the TIP4P/2005 model in the pressure-temperature plane (adapted from Fig. 9a of [2]) is given in a publication by Abascal, Sanz and Vega [3] (revisited by Conde et. al. [4]) and for negative pressures in the publication [5].
Liquid-vapour equilibria[edit]
Plastic crystal phases[edit]
Recent simulations have suggested the possibility of a plastic crystal phase or phases for water [2][7]
Supercooled region[edit]
The supercooled region has been studied by Abascal and Vega [8], locating a Widom line [9], indicating a second critical point for water located at 1350 bar and 193 K.
Surface tension[edit]
The surface tension has been studied for the TIP4P/2005 model, giving mJ/m2 at 300 K using the test area method [10], mN/m at 300 K using using the Ewald sums for the dispersion interactions [11], mJ/m2 at 350 K using the reaction field method [12] and mN/m at 249 K [13].
Self-diffusion coefficient[edit]
The TIP4P/2005 potential has a self-diffusion coefficient, in bulk water at 298 K, of 0.21 Å2 ps−1 in a classical simulation of 216 water molecules (experimental value: 0.23 Å2 ps−1) [14]. See also [15].
Shear viscosity[edit]
The shear viscosity for the TIP4P/2005 model is 0.855 mPa.s at 298 K and 1 bar [16] (experimental value 0.896 mPa.s [17]).
Liquid-liquid critical point[edit]
For the TIP4P/2005 model the liquid-liquid critical point is located at: K, MPa and having a density of kg/m3 [18]. K, MPa and having a density of kg/m3 [19].
Structure factor[edit]
The structure factor, in particular for small wave vectors, has been calculated by Sedlmeier, Horinek and Netz [20], who observe that the TIP4P/2005 model yields an "almost quantitative agreement".
Virial coefficients[edit]
The second virial coefficient has been calculated by Chialvo et al [21].
Thermal conductivity[edit]
Melting point[edit]
K [23].
References[edit]
- ↑ J. L. F. Abascal and C. Vega "A general purpose model for the condensed phases of water: TIP4P/2005", Journal of Chemical Physics, 123 234505 (2005)
- ↑ 2.0 2.1 J. L. Aragones and C. Vega "Plastic crystal phases of simple water models", Journal of Chemical Physics 130 244504 (2009)
- ↑ Jose L. F. Abascal, Eduardo Sanz and Carlos Vega "Triple points and coexistence properties of the dense phases of water calculated using computer simulation", Physical Chemistry Chemical Physics 11 pp. 556-562 (2009)
- ↑ M. M. Conde , M. A. Gonzalez , J. L. F. Abascal and C. Vega "Determining the phase diagram of water from direct coexistence simulations: The phase diagram of the TIP4P/2005 model revisited", Journal of Chemical Physics 139 154505 (2013)
- ↑ M. M. Conde, C. Vega, G. A. Tribello, and B. Slater "The phase diagram of water at negative pressures: Virtual ices", Journal of Chemical Physics 131 034510 (2009)
- ↑ C. Vega, J. L. F. Abascal and I. Nezbeda "Vapor-liquid equilibria from the triple point up to the critical point for the new generation of TIP4P-like models: TIP4P/Ew, TIP4P/2005, and TIP4P/ice" Journal of Chemical Physics 125 034503 (2006)
- ↑ J. L. Aragones, M. M. Conde, E. G. Noya and C. Vega "The phase diagram of water at high pressures as obtained by computer simulations of the TIP4P/2005 model: the appearance of a plastic crystal phase", Physical Chemistry Chemical Physics 11 pp. 543- (2009)
- ↑ J. L. F. Abascal and C. Vega "Note: Equation of state and compressibility of supercooled water: Simulations and experiment", Journal of Chemical Physics 134 186101 (2011)
- ↑ K. T. Wikfeldt, C. Huang, A. Nilsson, and L. G. M. Pettersson "Enhanced small-angle scattering connected to the Widom line in simulations of supercooled water", Journal of Chemical Physics 134 214506 (2011)
- ↑ C. Vega and E. de Miguel "Surface tension of the most popular models of water by using the test-area simulation method", Journal of Chemical Physics 126 154707 (2007)
- ↑ José Alejandre and Gustavo A. Chapela "The surface tension of TIP4P/2005 water model using Ewald sums for the dispersion interactions", Journal of Chemical Physics 132 014701 (2010)
- ↑ J. M. Míguez, D. González-Salgado, J. L. Legido, and M. M. Piñeiro "Calculation of interfacial properties using molecular simulation with the reaction field method: Results for different water models", Journal of Chemical Physics 132 184102 (2010)
- ↑ Ryuji Sakamaki, Amadeu K. Sum, Tetsu Narumi, and Kenji Yasuoka "Molecular dynamics simulations of vapor/liquid coexistence using the nonpolarizable water models", Journal of Chemical Physics 134 124708 (2011)
- ↑ Thomas E. Markland, Scott Habershon, and David E. Manolopoulos "Quantum diffusion of hydrogen and muonium atoms in liquid water and hexagonal ice", Journal of Chemical Physics 128 194506 (2008)
- ↑ Dmitri Rozmanov and Peter G. Kusalik "Transport coefficients of the TIP4P-2005 water model", Journal of Chemical Physics 136 044507 (2012)
- ↑ Miguel Angel González and José L. F. Abascal "The shear viscosity of rigid water models", Journal of Chemical Physics 132 096101 (2010)
- ↑ Kenneth R. Harris and Lawrence A. Woolf "Temperature and Volume Dependence of the Viscosity of Water and Heavy Water at Low Temperatures", Journal of Chemical & Engineering Data 49 pp. 1064-1069 (2004)
- ↑ José L. F. Abascal and Carlos Vega "Widom line and the liquid–liquid critical point for the TIP4P/2005 water model", Journal of Chemical Physics 133 234502 (2010)
- ↑ Rakesh S. Singh, John W. Biddle, Pablo G. Debenedetti and Mikhail A. Anisimov "Two-state thermodynamics and the possibility of a liquid-liquid phase transition in supercooled TIP4P/2005 water", Journal of Chemical Physics 144 144504 (2016)
- ↑ Felix Sedlmeier, Dominik Horinek, and Roland R. Netz "Spatial Correlations of Density and Structural Fluctuations in Liquid Water: A Comparative Simulation Study", Journal of the American Chemical Society Article ASAP (2011)
- ↑ Ariel A. Chialvo, Albert Bartók and András Baranyai "On the re-engineered TIP4P water models for the prediction of vapor–liquid equilibrium", Journal of Molecular Liquids 129 pp. 120-124 (2006)
- ↑ Frank Römer, Anders Lervik, and Fernando Bresme "Nonequilibrium molecular dynamics simulations of the thermal conductivity of water: A systematic investigation of the SPC/E and TIP4P/2005 models", Journal of Chemical Physics 137 074503 (2012)
- ↑ M. M. Conde, M. Rovere, and P. Gallo "High precision determination of the melting points of water TIP4P/2005 and water TIP4P/Ice models by the direct coexistence technique", Journal of Chemical Physics 147 244506 (2017)
Related reading
- Helena L. Pi, Juan L. Aragones, Carlos Vega, Eva G. Noya, Jose L. F. Abascal, Miguel A. Gonzalez and Carl McBride "Anomalies in water as obtained from computer simulations of the TIP4P/2005 model: density maxima, and density, isothermal compressibility and heat capacity minima", Molecular Physics 107 pp. 365-374 (2009)
- Miguel A. González, Chantal Valeriani, Frédéric Caupin and José L. F. Abascal "A comprehensive scenario of the thermodynamic anomalies of water using the TIP4P/2005 model", Journal of Chemical Physics 145 054505 (2016)
- Philip H. Handle and Francesco Sciortino "Potential energy landscape of TIP4P/2005 water", Journal of Chemical Physics 148 134505 (2018)