Critical points
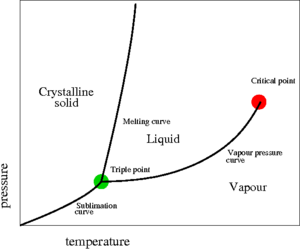
The critical point, discovered in 1822 by Charles Cagniard de la Tour [1][2] , is a point found at the end of the liquid-vapour coexistence curve (the red point shown on the pressure-temperature plot on the right). At this point the temperature is known as the critical temperature and the pressure is known as the critical pressure . For an interesting discourse on the "discovery" of the liquid-vapour critical point, the Bakerian Lecture of Thomas Andrews makes good reading [3]. Critical points are singularities in the partition function. In the critical point vicinity (Ref. [4] Eq. 17a)
and
For a review of the critical region see the work of Michael E. Fisher [5]
"... Turning now to the question of specific heats, it has long been known that real gases exhibit a large ``anomalous" specific-heat maximum above which lies near the critical isochore and which is not expected on classical theory..."
also
"... measurements (Ref. [6] ) of for argon along the critical isochore suggest strongly that . Such a result is again inconsistent with classical theory."
Thus in the vicinity of the liquid-vapour critical point, both the isothermal compressibility and the heat capacity at constant pressure diverge to infinity.
Liquid-liquid critical point[edit]
Solid-liquid critical point[edit]
It is widely held that there is no solid-liquid critical point. The reasoning behind this was given on the grounds of symmetry by Landau and Lifshitz [7]. However, recent work using the Z2 potential suggests that this may not be the last word on the subject. [8].
Tricritical points[edit]
- Robert B. Griffiths "Thermodynamics Near the Two-Fluid Critical Mixing Point in He3 - He4", Physical Review Letters 24 715-717 (1970)
- Lech Longa "On the tricritical point of the nematic–smectic A phase transition in liquid crystals", Journal of Chemical Physics 85 pp. 2974-2985 (1986)
Critical exponents[edit]
- Main article: Critical exponents
Yang-Yang anomaly[edit]
- Main article: Yang-Yang anomaly
See also[edit]
References[edit]
- ↑ Charles Cagniard de la Tour "Exposé de quelques résultats obtenu par l'action combinée de la chaleur et de la compression sur certains liquides, tels que l'eau, l'alcool, l'éther sulfurique et l'essence de pétrole rectifiée", Annales de chimie et de physique 21 pp. 127-132 (1822)
- ↑ Bertrand Berche, Malte Henkel, and Ralph Kenna "Critical phenomena: 150 years since Cagniard de la Tour", Revista Brasileira de Ensino de Física 31 pp.2602.1-2602.4 (2009) (in English arXiv:0905.1886v1)
- ↑ Thomas Andrews "The Bakerian Lecture: On the Continuity of the Gaseous and Liquid States of Matter", Philosophical Transactions of the Royal Society of London 159 pp. 575-590 (1869)
- ↑ G. A. Martynov; G. N. Sarkisov "Exact equations and the theory of liquids. V", Molecular Physics 49 pp. 1495-1504 (1983)
- ↑ Michael E. Fisher "Correlation Functions and the Critical Region of Simple Fluids", Journal of Mathematical Physics 5 pp. 944-962 (1964)
- ↑ A. Michels, J.M. Levelt and G.J. Wolkers "Thermodynamic properties of argon at temperatures between 0°C and −140°C and at densities up to 640 amagat (pressures up to 1050 atm.)", Physica 24 pp. 769-794 (1958)
- ↑ L. D. Landau and E. M. Lifshitz, "Statistical Physics" (Course of Theoretical Physics, Volume 5) 3rd Edition Part 1, Chapter XIV, Pergamon Press (1980) § 83 p. 258
- ↑ Måns Elenius and Mikhail Dzugutov "Evidence for a liquid-solid critical point in a simple monatomic system", Journal of Chemical Physics 131, 104502 (2009)
Related reading
- M. I. Bagatskii and A. V. Voronel and B. G. Gusak "", Journal of Experimental and Theoretical Physics 16 pp. 517- (1963)
- Robert B. Griffiths and John C. Wheeler "Critical Points in Multicomponent Systems", Physical Review A 2 1047 - 1064 (1970)
- Michael E. Fisher "The renormalization group in the theory of critical behavior", Reviews of Modern Physics 46 pp. 597 - 616 (1974)
- J. V. Sengers and J. M. H. Levelt Sengers "Thermodynamic Behavior of Fluids Near the Critical Point", Annual Review of Physical Chemistry 37 pp. 189-222 (1986)
- Kamakshi Jagannathan and Arun Yethiraj "Molecular Dynamics Simulations of a Fluid near Its Critical Point", Physical Review Letters 93 015701 (2004)
- Kurt Binder "Computer simulations of critical phenomena and phase behaviour of fluids", Molecular Physics 108 pp. 1797-1815 (2010)
- Books
- H. Eugene Stanley "Introduction to Phase Transitions and Critical Phenomena", Oxford University Press (1971) ISBN 9780195053166
- Cyril Domb "The Critical Point: A Historical Introduction To The Modern Theory Of Critical Phenomena", Taylor and Francis (1996) ISBN 9780748404353






