Lennard-Jones model
The Lennard-Jones intermolecular pair potential is a special case of the Mie potential and takes its name from Sir John Edward Lennard-Jones [1] [2]. The Lennard-Jones model consists of two 'parts'; a steep repulsive term, and smoother attractive term, representing the London dispersion forces [3]. The Lennard-Jones potential is probably the most extensively studied model potential today [4]. Apart from being an important model in itself, the Lennard-Jones potential frequently forms one of 'building blocks' of many force fields and molecular-based equation of state models [5]. It is worth mentioning that the 12-6 Lennard-Jones model is not the most faithful representation of the potential energy surface, but rather its use is widespread due to its computational expediency. For example, the repulsive term is maybe better described with the exp-6 potential. One of the first computer simulations using the Lennard-Jones model was undertaken by Wood and Parker in 1957 [6] in a study of liquid argon. Thermophysical property data sampled by molecular simulations since then until 2019 has been compiled, digitalized and assessed by Stephan et al [4]. This database contains about 35,000 datapoints.
Functional form
The Lennard-Jones potential is given by
or is sometimes expressed as
where
- is the intermolecular pair potential between two particles or sites
- is the value of at which
- is the well depth (energy)
- ,
- Minimum value of at ;
In reduced units:
- Density:
where (number of particles divided by the volume )
- Temperature:
where is the absolute temperature and is the Boltzmann constant
The following is a plot of the Lennard-Jones model for the Rowley, Nicholson and Parsonage parameter set [7] ( 119.8 K and 0.3405 nm). See argon for other parameter sets.
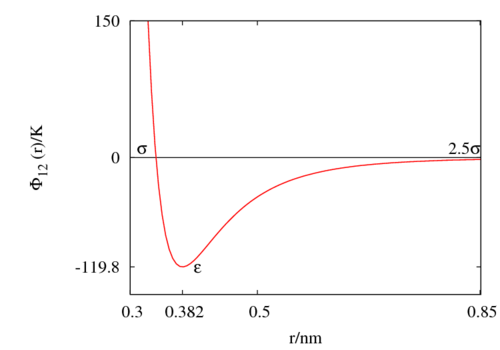
Critical point
The location of the critical point for the untruncated potential has been assessed to be at [4]
at a reduced density of
and the critical pressure of
The critical compressibility factor is given by [8]
Vliegenthart and Lekkerkerker [9] [10] have suggested that the critical point is related to the second virial coefficient via the expression
Truncated at
For the potential truncated at [11]
Triple point
The location of the triple point as found by Mastny and de Pablo [12] is
- (liquid);
- (solid).
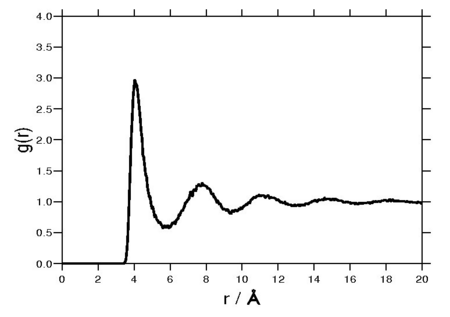
Radial distribution function
The following plot is of a typical radial distribution function for the monatomic Lennard-Jones liquid[13] (here with Å and kcal/mol at a temperature of 111.06K):
Helmholtz energy function
An expression for the Helmholtz energy function of the face centred cubic solid has been given by van der Hoef [14], applicable within the density range and the temperature range . For the liquid state see the work of Johnson, Zollweg and Gubbins [15].
Vapor-liquid equilibrium
The vapor-liquid equilibrium of the Lennard-Jones potential has been studied more than 45 times in the literature. Several of these data sets were found to have gross deviations to an entity of data sets, which is both thermodynamically consistent and in good mutual agreement [4]. The mutual agreement of these data sets was found to be approximately for the vapor pressure, for the enthalpy of vaporization, for the saturated liquid density, and for the saturated vapor density [4].
Melting line
The solid and liquid densities along the melting line [16] are given by the following equations:
van der Hoef
van der Hoef (Ref. [17] Eqs. 25 and 26):
and
Mastny and de Pablo
Mastny and de Pablo (Ref [18] Eqs. 20 and 21):
and
A study has been performed of the solid-fluid equilibria, and behavior in the high density region [19].
Zeno line
It has been shown that the Lennard-Jones model has a straight Zeno line [20] on the density-temperature plane.
Widom line
It has been shown that the Lennard-Jones model has a Widom line [21] on the pressure-temperature plane.
Viscosity
Perturbation theory
The Lennard-Jones model is also used in perturbation theories, for example see: Weeks-Chandler-Andersen perturbation theory.
Approximations in simulation: truncation and shifting
The Lennard-Jones model is often used with a cutoff radius of , beyond which is set to zero. Setting the well depth to be 1 in the potential on arrives at , i.e. at this distance the potential is at less than 2% of the well depth. For an analysis of the effect of this cutoff on the melting line see the work of Mastny and de Pablo [12] and of Ahmed and Sadus [23]. See Panagiotopoulos for critical parameters [24]. See Pártay for the ground state structure [25]. It has recently been suggested that a truncated and shifted force cutoff of can be used under certain conditions [26]. In order to avoid any discontinuity, a piecewise continuous version, known as the modified Lennard-Jones model, was developed.
Cutoff Lennard-Jones potential
The cutoff Lennard-Jones potential is given by (Eq. 2 in [27]):
where is the cutoff radius.
n-m Lennard-Jones potential
It is relatively common to encounter potential functions given by:
with and being positive integers and .
is chosen such that the minimum value of being .
Such forms are usually referred to as n-m Lennard-Jones Potential.
For example, the 9-3 Lennard-Jones interaction potential is often used to model the interaction between
a continuous solid wall and the atoms/molecules of a liquid.
On the '9-3 Lennard-Jones potential' page a justification of this use is presented. Another example is the n-6 Lennard-Jones potential,
where is fixed at 6, and is free to adopt a range of integer values.
The potentials form part of the larger class of potentials known as the Mie potential.
Examples:
- 8-6 Lennard-Jones potential
- 9-3 Lennard-Jones potential
- 9-6 Lennard-Jones potential
- 10-4-3 Lennard-Jones potential
- 200-100 Lennard-Jones potential
- n-6 Lennard-Jones potential
Equation of state
- Main article: Lennard-Jones equation of state
Virial coefficients
- Main article: Lennard-Jones model: virial coefficients
Phase diagram
- Main article: Phase diagram of the Lennard-Jones model
Related models
- Kihara potential
- Lennard-Jones model in 1-dimension (rods)
- Lennard-Jones model in 2-dimensions (disks)
- Lennard-Jones model in 4-dimensions
- Lennard-Jones sticks
- Mie potential
- Soft-core Lennard-Jones model
- Soft sphere potential
- Stockmayer potential
- Mixtures
References
- ↑ John Edward Lennard-Jones "On the Determination of Molecular Fields. I. From the Variation of the Viscosity of a Gas with Temperature", Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character 106 pp. 441-462 (1924) § 8 (ii)
- ↑ John Edward Lennard-Jones "On the Determination of Molecular Fields. II. From the Equation of State of a Gas", Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character 106 pp. 463-477 (1924) Eq. 2.05
- ↑ F. London "Zur Theorie und Systematik der Molekularkräfte", Zeitschrift für Physik A Hadrons and Nuclei 63 pp. 245-279 (1930)
- ↑ 4.0 4.1 4.2 4.3 4.4 Simon Stephan, Monika Thol, Jadran Vrabec, and Hans Hasse "Thermophysical Properties of the Lennard-Jones Fluid: Database and Data Assessment", Journal of Chemical Information and Modeling 59, 10 pp. 4248–4265 (2019)
- ↑ Simon Stephan, Jens Staubach, Hans Hasse "Review and comparison of equations of state for the Lennard-Jones fluid", Fluid Phase Equilibria 523 pp. 112772 (2020)
- ↑ W. W. Wood and F. R. Parker "Monte Carlo Equation of State of Molecules Interacting with the Lennard‐Jones Potential. I. A Supercritical Isotherm at about Twice the Critical Temperature", Journal of Chemical Physics 27 pp. 720- (1957)
- ↑ L. A. Rowley, D. Nicholson and N. G. Parsonage "Monte Carlo grand canonical ensemble calculation in a gas-liquid transition region for 12-6 Argon", Journal of Computational Physics 17 pp. 401-414 (1975)
- ↑ V. L. Kulinskii "The critical compressibility factor of fluids from the global isomorphism approach", Journal of Chemical Physics 139 184119 (2013)
- ↑ G. A. Vliegenthart and H. N. W. Lekkerkerker "Predicting the gas–liquid critical point from the second virial coefficient", Journal of Chemical Physics 112 pp. 5364-5369 (2000)
- ↑ L. A. Bulavin and V. L. Kulinskii "Generalized principle of corresponding states and the scale invariant mean-field approach", Journal of Chemical Physics '133 134101 (2010)
- ↑ Ernesto S. Loscar, C. Gastón Ferrara1, and Tomás S. Grigera "Spinodals and critical point using short-time dynamics for a simple model of liquid", Journal of Chemical Physics 144 134501 (2016)
- ↑ 12.0 12.1 Ethan A. Mastny and Juan J. de Pablo "Melting line of the Lennard-Jones system, infinite size, and full potential", Journal of Chemical Physics 127 104504 (2007)
- ↑ John G. Kirkwood, Victor A. Lewinson, and Berni J. Alder "Radial Distribution Functions and the Equation of State of Fluids Composed of Molecules Interacting According to the Lennard-Jones Potential", Journal of Chemical Physics 20 pp. 929- (1952)
- ↑ Martin A. van der Hoef "Free energy of the Lennard-Jones solid", Journal of Chemical Physics 113 pp. 8142-8148 (2000)
- ↑ J. Karl Johnson, John A. Zollweg and Keith E. Gubbins "The Lennard-Jones equation of state revisited", Molecular Physics 78 pp. 591-618 (1993)
- ↑ D. M. Heyes and A. C. Brańka "The Lennard-Jones melting line and isomorphism", Journal of Chemical Physics 143 234504 (2015)
- ↑ Martin A. van der Hoef "Free energy of the Lennard-Jones solid", Journal of Chemical Physics 113 pp. 8142-8148 (2000)
- ↑ Ethan A. Mastny and Juan J. de Pablo "Melting line of the Lennard-Jones system, infinite size, and full potential", Journal of Chemical Physics 127 104504 (2007)
- ↑ Andreas Köster, Peter Mausbach, and Jadran Vrabec "Premelting, solid-fluid equilibria, and thermodynamic properties in the high density region based on the Lennard-Jones potential", Journal of Chemical Physics 147 144502 (2017)
- ↑ E. M. Apfelbaum, V. S. Vorob’ev and G. A. Martynov "Regarding the Theory of the Zeno Line", Journal of Physical Chemistry A 112 pp. 6042-6044 (2008)
- ↑ V. V. Brazhkin, Yu. D. Fomin, A. G. Lyapin, V. N. Ryzhov, and E. N. Tsiok "Widom Line for the Liquid–Gas Transition in Lennard-Jones System", Journal of Physical Chemistry B Article ASAP (2011)
- ↑ Kai-Min Tu,  Kang Kim, and  Nobuyuki Matubayasi "Spatial-decomposition analysis of viscosity with application to Lennard-Jones fluid", Journal of Chemical Physics 148 094501 (2018)
- ↑ Alauddin Ahmed and Richard J. Sadus "Effect of potential truncations and shifts on the solid-liquid phase coexistence of Lennard-Jones fluids", Journal of Chemical Physics 133 124515 (2010)
- ↑ A. Z. Panagiotopoulos "Molecular simulation of phase coexistence: Finite-size effects and determination of critical parameters for two- and three-dimensional Lennard-Jones fluids", International Journal of Thermophysics 15 pp. 1057-1072 (1994)
- ↑ Lívia B. Pártay, Christoph Ortner, Albert P. Bartók, Chris J. Pickard and Gábor Csányi "Polytypism in the ground state structure of the Lennard-Jonesium", Physical Chemistry Chemical Physics 19 19369 (2017)
- ↑ Søren Toxvaerd and Jeppe C. Dyre "Communication: Shifted forces in molecular dynamics", Journal of Chemical Physics 134 081102 (2011)
- ↑ Spotswood D. Stoddard and Joseph Ford "Numerical Experiments on the Stochastic Behavior of a Lennard-Jones Gas System", Physical Review A 8 pp. 1504-1512 (1973)
![{\displaystyle \Phi _{12}(r)=4\epsilon \left[\left({\frac {\sigma }{r}}\right)^{12}-\left({\frac {\sigma }{r}}\right)^{6}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc9f91d43a2f39f321b2054db022e07ae7c29988)






































![{\displaystyle \ln p^{s}=n_{1}T+{\frac {n_{2}}{T}}+{\frac {n_{3}}{T^{n_{4}}}}~~\mathrm {with} ~~n_{i}=[1.156551,-4.431519,-0.423028,2.638743]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8cdf1c7e314dfa66b717262ed20deb8929f4aed4)
![{\displaystyle {\Big (}{\frac {\rho '}{\rho _{\mathrm {c} }}}{\Big )}=1+\sum _{i=1}^{5}n_{i}\,{\Big (}1-{\frac {T}{T_{\mathrm {c} }}}{\Big )}^{t_{i}}~~\mathrm {with} ~~n_{i}=[1.3417,2.075332,-2.123475,0.328998,1.386131]~~\&~~t_{i}=[0.32714,0.958759,1.645654,17.000001,2.400858]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/579bba58f1e070993261409af3923aacdb7fbf37)
![{\displaystyle \ln {\Big (}{\frac {\rho ''}{\rho _{\mathrm {c} }}}{\Big )}=\sum _{i=1}^{5}n_{i}\,{\Big (}1-{\frac {T}{T_{\mathrm {c} }}}{\Big )}^{t_{i}}~~\mathrm {with} ~~n_{i}=[-8.135822,-102.91911,-3.037979,-44.381841,-34.55892948]~~\&~~t_{i}=[1.651685,43.469214,0.462877,11.500462,5.39437]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d764f34334ed7c0f261a513c96fd4a02ec7b80ec)
![{\displaystyle \Delta h_{v}=\sum _{i=1}^{4}n_{i}\,(T_{\mathrm {c} }-T)^{t_{i}}~~\mathrm {with} ~~n_{i}=[6.456728,2.700099,-3.073573,3.149052]~~\&~~t_{i}=[0.411342,0.460416,2.350953,5.01701]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/372e667017ad4c12b59d126c0b02377eb748e4d1)
![{\displaystyle \rho _{\mathrm {solid} }=\beta ^{-1/4}\left[0.92302-0.09218\beta +0.62381\beta ^{2}-0.82672\beta ^{3}+0.49124\beta ^{4}-0.10847\beta ^{5}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ff07fecb196ca0daf4d0e31d6bb46f00b3c48a01)
![{\displaystyle \rho _{\mathrm {liquid} }=\beta ^{-1/4}\left[0.91070-0.25124\beta +0.85861\beta ^{2}-1.08918\beta ^{3}+0.63932\beta ^{4}-0.14433\beta ^{5}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c40a60cc9f93746398f05f81f31befb77262284)
![{\displaystyle \rho _{\mathrm {solid} }=\beta ^{-1/4}\left[0.908629-0.041510\beta +0.514632\beta ^{2}-0.708590\beta ^{3}+0.428351\beta ^{4}-0.095229\beta ^{5}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9d42739dd208f4ac0bb02525ea454ca8598593fd)
![{\displaystyle \rho _{\mathrm {liquid} }=\beta ^{-1/4}\left[0.90735-0.27120\beta +0.91784\beta ^{2}-1.16270\beta ^{3}+0.68012\beta ^{4}-0.15284\beta ^{5}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f25d53a5319a238d2c5b4ace3f32f59054dea660)


![{\displaystyle \Phi _{12}(r)=4\epsilon \left\{\left[\left({\frac {\sigma }{r}}\right)^{12}-\left({\frac {\sigma }{r}}\right)^{6}\right]+\left[6\left({\frac {\sigma }{r_{c}}}\right)^{12}-3\left({\frac {\sigma }{r_{c}}}\right)^{6}\right]\left({\frac {r}{r_{c}}}\right)^{2}-7\left({\frac {\sigma }{r_{c}}}\right)^{12}+4\left({\frac {\sigma }{r_{c}}}\right)^{6}\right\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bdf89db70296ef8cdf41052fe97df8e84b94f059)

![{\displaystyle \Phi _{12}(r)=c_{n,m}\epsilon \left[\left({\frac {\sigma }{r}}\right)^{n}-\left({\frac {\sigma }{r}}\right)^{m}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a7ef03a3a6ed92cc384a523b885962611ded7719)




