Lennard-Jones model: Difference between revisions
Carl McBride (talk | contribs) m (→Zeno line) |
Carl McBride (talk | contribs) (Started a section on the Helmholtz energy function) |
||
| Line 46: | Line 46: | ||
:<math>\rho_{tp}^* = 0.84</math> (liquid); <math>\rho_{tp}^* = 0.96</math> (solid) | :<math>\rho_{tp}^* = 0.84</math> (liquid); <math>\rho_{tp}^* = 0.96</math> (solid) | ||
==Radial distribution function== | |||
The following plot is of a typical [[radial distribution function]] for the monatomic Lennard-Jones liquid<ref>[http://dx.doi.org/10.1063/1.1700653 John G. Kirkwood, Victor A. Lewinson, and Berni J. Alder "Radial Distribution Functions and the Equation of State of Fluids Composed of Molecules Interacting According to the Lennard-Jones Potential", Journal of Chemical Physics '''20''' pp. 929- (1952)]</ref> (here with <math>\sigma=3.73 {\mathrm {\AA}}</math> and <math>\epsilon=0.294</math> kcal/mol at a [[temperature]] of 111.06K): | |||
[[Image:LJ_rdf.png|center|450px|Typical radial distribution function for the monatomic Lennard-Jones liquid.]] | |||
==Helmholtz energy function== | |||
An expression for the [[Helmholtz energy function]] of the [[Building up a face centered cubic lattice | face centred cubic]] solid has been given by van der Hoef <ref>[http://dx.doi.org/10.1063/1.1314342 Martin A. van der Hoef "Free energy of the Lennard-Jones solid", Journal of Chemical Physics '''113''' pp. 8142-8148 (2000)]</ref>, applicable within the density range <math>0.94 \le \rho^* \le 1.20</math> and the temperature range <math>0.1 \le T^* \le 2.0</math>. For the liquid state see <ref>[http://dx.doi.org/10.1080/00268979300100411 J. Karl Johnson, John A. Zollweg and Keith E. Gubbins "The Lennard-Jones equation of state revisited", Molecular Physics '''78''' pp. 591-618 (1993)]</ref>. | |||
==Equation of state== | |||
:''Main article: [[Lennard-Jones equation of state]]'' | |||
==Virial coefficients== | |||
:''Main article: [[Lennard-Jones model: virial coefficients]]'' | |||
==Phase diagram== | |||
:''Main article: [[Phase diagram of the Lennard-Jones model]]'' | |||
==Zeno line== | |||
It has been shown that the Lennard-Jones model has a straight [[zeno line]] <ref>[http://dx.doi.org/10.1021/jp802999z E. M. Apfelbaum, V. S. Vorob’ev and G. A. Martynov "Regarding the Theory of the Zeno Line", Journal of Physical Chemistry A '''112''' pp. 6042-6044 (2008)]</ref> on the [[Phase diagrams: Density-temperature plane |density−temperature plane]]. | |||
==Perturbation theory== | |||
The Lennard-Jones model is also used in [[Perturbation theory |perturbation theories]], for example see: [[Weeks-Chandler-Anderson perturbation theory]]. | |||
== Approximations in simulation: truncation and shifting == | == Approximations in simulation: truncation and shifting == | ||
The Lennard-Jones model is often used with a cutoff radius of <math>2.5 \sigma</math>, beyond which <math> \Phi_{12}(r)</math> is set to zero. Setting the well depth <math> \epsilon </math> to be 1 in the potential on arrives at <math> \Phi_{12}(r)\simeq -0.0163</math>, i.e. at this distance the potential is at less than 2% of the well depth. For an analysis of the effect of this cutoff on the melting line see the work of Mastny and de Pablo <ref name="Mastny"> </ref> and of | The Lennard-Jones model is often used with a cutoff radius of <math>2.5 \sigma</math>, beyond which <math> \Phi_{12}(r)</math> is set to zero. Setting the well depth <math> \epsilon </math> to be 1 in the potential on arrives at <math> \Phi_{12}(r)\simeq -0.0163</math>, i.e. at this distance the potential is at less than 2% of the well depth. For an analysis of the effect of this cutoff on the melting line see the work of Mastny and de Pablo <ref name="Mastny"> </ref> and of Ahmed and Sadus <ref>[http://dx.doi.org/10.1063/1.3481102 Alauddin Ahmed and Richard J. Sadus "Effect of potential truncations and shifts on the solid-liquid phase coexistence of Lennard-Jones fluids", Journal of Chemical Physics '''133''' 124515 (2010)]</ref>. See Panagiotopoulos for critical parameters <ref>[http://dx.doi.org/10.1007/BF01458815 A. Z. Panagiotopoulos "Molecular simulation of phase coexistence: Finite-size effects and determination of critical parameters for two- and three-dimensional Lennard-Jones fluids", International Journal of Thermophysics '''15''' pp. 1057-1072 (1994)]</ref>. | ||
== n-m Lennard-Jones potential == | == n-m Lennard-Jones potential == | ||
| Line 63: | Line 78: | ||
where <math>m</math> is fixed at 6, and <math>n</math> is free to adopt a range of integer values. | where <math>m</math> is fixed at 6, and <math>n</math> is free to adopt a range of integer values. | ||
The potentials form part of the larger class of potentials known as the [[Mie potential]]. | The potentials form part of the larger class of potentials known as the [[Mie potential]]. | ||
<br> | |||
Examples: | |||
*[[8-6 Lennard-Jones potential]] | *[[8-6 Lennard-Jones potential]] | ||
*[[9-3 Lennard-Jones potential]] | *[[9-3 Lennard-Jones potential]] | ||
| Line 69: | Line 85: | ||
*[[10-4-3 Lennard-Jones potential]] | *[[10-4-3 Lennard-Jones potential]] | ||
*[[n-6 Lennard-Jones potential]] | *[[n-6 Lennard-Jones potential]] | ||
==Mixtures== | ==Mixtures== | ||
*[[Binary Lennard-Jones mixtures]] | *[[Binary Lennard-Jones mixtures]] | ||
Revision as of 15:46, 23 November 2010
The Lennard-Jones intermolecular pair potential is a special case of the Mie potential and takes its name from Sir John Edward Lennard-Jones [1] [2]. The Lennard-Jones model consists of two 'parts'; a steep repulsive term, and smoother attractive term, representing the London dispersion forces. Apart from being an important model in itself, the Lennard-Jones potential frequently forms one of 'building blocks' of many force fields. It is worth mentioning that the 12-6 Lennard-Jones model is not the most faithful representation of the potential energy surface, but rather its use is widespread due to its computational expediency. For example, the repulsive term is maybe better described with the exp-6 potential. One of the first computer simulations using the Lennard-Jones model was undertaken by Rahman in 1964 [3] in a study of liquid argon.
Functional form
The Lennard-Jones potential is given by
![{\displaystyle \Phi _{12}(r)=4\epsilon \left[\left({\frac {\sigma }{r}}\right)^{12}-\left({\frac {\sigma }{r}}\right)^{6}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc9f91d43a2f39f321b2054db022e07ae7c29988)
where
- is the intermolecular pair potential between two particles or sites
- is the value of at which
- is the well depth (energy)
In reduced units:
- Density: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho^* := \rho \sigma^3 } , where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho := N/V } (number of particles Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N } divided by the volume Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V } )
- Temperature: Failed to parse (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle T^{*}:=k_{B}T/\epsilon } , where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T } is the absolute temperature and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_B } is the Boltzmann constant
The following is a plot of the Lennard-Jones model for the Rowley, Nicholson and Parsonage parameter set [4] (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon/k_B = }
119.8 K and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma=}
0.3405 nm). See argon for other parameter sets.
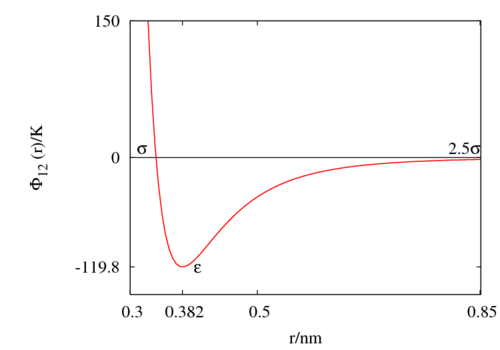
Special points
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi_{12}(\sigma) = 0 }
- Minimum value of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi_{12}(r) } at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r = r_{min} } ;
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{r_{min}}{\sigma} = 2^{1/6} \simeq 1.12246 ... }
Critical point
The location of the critical point is [5]
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_c^* = 1.326 \pm 0.002}
at a reduced density of
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho_c^* = 0.316 \pm 0.002} .
Vliegenthart and Lekkerkerker [6] [7] have suggested that the critical point is related to the second virial coefficient via the expression
- Failed to parse (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle B_{2}\vert _{T=T_{c}}=-\pi \sigma ^{3}}
Triple point
The location of the triple point as found by Mastny and de Pablo [8] is
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_{tp}^* = 0.694}
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho_{tp}^* = 0.84} (liquid); Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho_{tp}^* = 0.96} (solid)
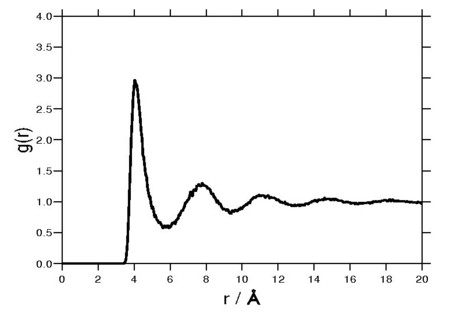
Radial distribution function
The following plot is of a typical radial distribution function for the monatomic Lennard-Jones liquid[9] (here with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma=3.73 {\mathrm {\AA}}} and kcal/mol at a temperature of 111.06K):
Helmholtz energy function
An expression for the Helmholtz energy function of the face centred cubic solid has been given by van der Hoef [10], applicable within the density range Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0.94 \le \rho^* \le 1.20} and the temperature range Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0.1 \le T^* \le 2.0} . For the liquid state see [11].
Equation of state
- Main article: Lennard-Jones equation of state
Virial coefficients
- Main article: Lennard-Jones model: virial coefficients
Phase diagram
- Main article: Phase diagram of the Lennard-Jones model
Zeno line
It has been shown that the Lennard-Jones model has a straight zeno line [12] on the density−temperature plane.
Perturbation theory
The Lennard-Jones model is also used in perturbation theories, for example see: Weeks-Chandler-Anderson perturbation theory.
Approximations in simulation: truncation and shifting
The Lennard-Jones model is often used with a cutoff radius of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2.5 \sigma} , beyond which Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi_{12}(r)} is set to zero. Setting the well depth Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon } to be 1 in the potential on arrives at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi_{12}(r)\simeq -0.0163} , i.e. at this distance the potential is at less than 2% of the well depth. For an analysis of the effect of this cutoff on the melting line see the work of Mastny and de Pablo [8] and of Ahmed and Sadus [13]. See Panagiotopoulos for critical parameters [14].
n-m Lennard-Jones potential
It is relatively common to encounter potential functions given by:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi_{12}(r) = c_{n,m} \epsilon \left[ \left( \frac{ \sigma }{r } \right)^n - \left( \frac{\sigma}{r} \right)^m \right]. }
with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n }
and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m }
being positive integers and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n > m }
.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c_{n,m} }
is chosen such that the minimum value of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi_{12}(r) }
being .
Such forms are usually referred to as n-m Lennard-Jones Potential.
For example, the 9-3 Lennard-Jones interaction potential is often used to model the interaction between
the atoms/molecules of a fluid and a continuous solid wall.
On the '9-3 Lennard-Jones potential' page a justification of this use is presented. Another example is the n-6 Lennard-Jones potential,
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m}
is fixed at 6, and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n}
is free to adopt a range of integer values.
The potentials form part of the larger class of potentials known as the Mie potential.
Examples:
- 8-6 Lennard-Jones potential
- 9-3 Lennard-Jones potential
- 9-6 Lennard-Jones potential
- 10-4-3 Lennard-Jones potential
- n-6 Lennard-Jones potential
Mixtures
Related models
- Kihara potential
- Lennard-Jones model in 1-dimension (rods)
- Lennard-Jones model in 2-dimensions (disks)
- Lennard-Jones model in 4-dimensions
- Lennard-Jones sticks
- Mie potential
- Soft-core Lennard-Jones model
- Soft sphere potential
- Stockmayer potential
References
- ↑ John Edward Lennard-Jones "On the Determination of Molecular Fields. I. From the Variation of the Viscosity of a Gas with Temperature", Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character 106 pp. 441-462 (1924) § 8 (ii)
- ↑ John Edward Lennard-Jones "On the Determination of Molecular Fields. II. From the Equation of State of a Gas", Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character 106 pp. 463-477 (1924) Eq. 2.05
- ↑ A. Rahman "Correlations in the Motion of Atoms in Liquid Argon", Physical Review 136 pp. A405–A411 (1964)
- ↑ L. A. Rowley, D. Nicholson and N. G. Parsonage "Monte Carlo grand canonical ensemble calculation in a gas-liquid transition region for 12-6 Argon", Journal of Computational Physics 17 pp. 401-414 (1975)
- ↑ J. M. Caillol " Critical-point of the Lennard-Jones fluid: A finite-size scaling study", Journal of Chemical Physics 109 pp. 4885-4893 (1998)
- ↑ G. A. Vliegenthart and H. N. W. Lekkerkerker "Predicting the gas–liquid critical point from the second virial coefficient", Journal of Chemical Physics 112 pp. 5364-5369 (2000)
- ↑ L. A. Bulavin and V. L. Kulinskii "Generalized principle of corresponding states and the scale invariant mean-field approach", Journal of Chemical Physics '133 134101 (2010)
- ↑ 8.0 8.1 Ethan A. Mastny and Juan J. de Pablo "Melting line of the Lennard-Jones system, infinite size, and full potential", Journal of Chemical Physics 127 104504 (2007)
- ↑ John G. Kirkwood, Victor A. Lewinson, and Berni J. Alder "Radial Distribution Functions and the Equation of State of Fluids Composed of Molecules Interacting According to the Lennard-Jones Potential", Journal of Chemical Physics 20 pp. 929- (1952)
- ↑ Martin A. van der Hoef "Free energy of the Lennard-Jones solid", Journal of Chemical Physics 113 pp. 8142-8148 (2000)
- ↑ J. Karl Johnson, John A. Zollweg and Keith E. Gubbins "The Lennard-Jones equation of state revisited", Molecular Physics 78 pp. 591-618 (1993)
- ↑ E. M. Apfelbaum, V. S. Vorob’ev and G. A. Martynov "Regarding the Theory of the Zeno Line", Journal of Physical Chemistry A 112 pp. 6042-6044 (2008)
- ↑ Alauddin Ahmed and Richard J. Sadus "Effect of potential truncations and shifts on the solid-liquid phase coexistence of Lennard-Jones fluids", Journal of Chemical Physics 133 124515 (2010)
- ↑ A. Z. Panagiotopoulos "Molecular simulation of phase coexistence: Finite-size effects and determination of critical parameters for two- and three-dimensional Lennard-Jones fluids", International Journal of Thermophysics 15 pp. 1057-1072 (1994)