Computation of phase equilibria
The computation of phase equilibria using computer simulation can follow a number of different strategies. Here we will focus mainly on first-order transitions in fluid phases, usually liquid-vapour equilibria. Thermodynamic equilibrium implies, for two phases and :
- equal temperatures:
- equal pressures:
- equal chemical potentials:
Independent simulations for each phase at fixed temperature in the canonical ensemble[edit]
Simulations can be carried out using either the Monte Carlo or the molecular dynamics technique. Assuming that one has some knowledge on the phase diagram of the system, one can try the following recipe:
- Fix a temperature and a number of particles
- Perform a limited number of simulations in the low density region (where the gas phase density is expected to be)
- Perform a limited number of simulations in the moderate to high density region (where the liquid phase should appear)
- In these simulations we can compute for each density (at fixed temperature) the values of the pressure and the chemical potentials (for instance using the Widom test-particle method)
A quick 'first guess' method[edit]
Using the previously obtained results the following, somewhat unsophisticated, procedure can be used to obtain a first inspection of the possible phase equilibrium:
- Fit the simulation results for each branch by using appropriate functional forms:
- Use the fits to build, for each phase, a table with three entries: , then plot for both tables as a function of and check to see if the two lines intersect.
- The crossing point provides (to within statistical uncertainty, the errors due to finite size effects, etc.) the coexistence conditions.
Improving the 'first guess' method[edit]
It can be useful to take into account classical thermodynamics to improve the previous analysis. This is because is is not unusual have large uncertainties in the results for the properties. The basic idea is to use thermodynamic consistency requirements to improve the analysis.
Methodology in the NpT ensemble[edit]
Low temperature: [edit]
For temperatures well below the critical point, provided that the calculation of the chemical potential of the liquid phase using Widom test-particle method gives precise results, the following strategy can be used to obtain a 'quick' result:
- Perform an simulation of the liquid phase at zero pressure, i.e.
- Arrive at an initial estimate, for the coexistence value of the chemical potential by computing, in the liquid phase:
- Make a first estimate of the coexistence pressure, , by computing, either via simulation or via the virial coefficients of the gas phase, the pressure at which the gas phase fulfils:
- Refine the results, if required, by performing a simulation of the liquid phase at , or use estimates of (from the initial simulation) and the gas equation of state data to correct the initial estimates of pressure and chemical potential at coexistence.
Note that this method works only if the liquid phase remains metastable at zero pressure.
Weak first order transitions[edit]
There are situations where other strategies based on NpT ensemble simulations can be used. Similar approaches have also been applied in the Grand Canonical ensemble. In practice, the free energy barrier between the two phases has to be low enough to allow the simulated system to cross from one phase to the other when it is being simulated. Somehow, the situation is now the opposite to that described in Section 2.1. Taking into the account the classical partition function in the NpT ensemble it can be written:
- ,
where stands for the probability of the volume at given conditions . Let the pressure at which the phase transition occurs. In such a case the following scenario is expected for :
- has two maxima, corresponding to the liquid and vapor pure phases, with
- The probability of a given intermediate volume at can be estimated (from macroscopic arguments) as:
- ,
where is the surface tension of the vapor-liquid interface, and is the surface area, which depends on the thermodynamic variables and the geometry of the simulation box. For small values of the surface tension, small system sizes and good simulation algorithms it could be possible for pressures close to to sample in a simulation the whole region of densities between vapour and liquid densities. If such is the case the phase equilibria conditions can be computed by reweighing techniques applied on the volume histograms of the simulation.
Simple reweighing of the volume probability distribution[edit]
Suppose that a precise simulation has been carried out at pressure . From that simulation a volume probability distribution, has been computed. It is possible to use this function to estimate the distributions of volume for pressure values close to ;
Using this reweighing procedure we can estimate the value of ; that is: the value of pressure for which the volume distribution presents two peaks of equal height. The analysis of the form of the distributions at the equilibrium conditions for different system sizes (i.e. in the current case for different values of ) can be useful to distinguish between continuous and first order phase transitions.
See also[edit]
Van der Waals loops in the canonical ensemble[edit]
It is possible to compute the liquid-vapour equilibrium without explicit calculations of the chemical potential (or the pressure) by performing a number of simulations sampling appropriately the vapour, liquid, and intermediate regions. As an example, consider a simple fluid at a given subcritical temperature (). We can perform a number of simulations for a given number of particles, and different densities:
In these simulations, we can compute the pressure (or the chemical potential) and fit the result to an appropriate equation. With such an equation of state the phase equilibria can be estimated. If two phase equilibria exists, a loop in the representation of (or ) should appear.
- Computing from the equation of state given as :
For fixed temperature and number of particles:
where is the Helmholtz energy function and , integrating:
On the other hand
therefore:
A similar procedure can be built up to compute from . Once and are known it is straightforward to compute the coexistence point.
Practical details[edit]
Some precautions should be taken if this procedure is used:
- The precision of the simulation results in the two phase region will be poor (so, large simulations are required to have a good estimation of the equation of state)
- The simulation results in the two phase region will depend dramatically on the system size (calculations with different number of particles become convenient to check the quality of the phase equilibria results)
Direct simulation of the two phase system[edit]
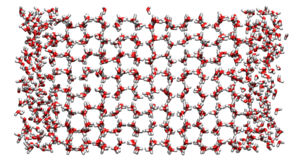
Direct simulation of the two phase system was first implemented by Abraham [1]. It has since been applied to the Lennard-Jones model [2] and water [3].
Gibbs ensemble Monte Carlo for one component systems[edit]
The Gibbs ensemble Monte Carlo method is often considered as a smart variation of the standard canonical ensemble procedure (See [4]). The simulation is, therefore, carried out at constant volume, temperature and number of particles. The whole system is divided into two non-interacting parts, each one has its own simulation box with its own periodic boundary conditions. This separation of the two phases into different boxes is in order to suppress any influence due to interfacial effects. The two subsystems can interchange volume and particles. The rules for these interchanges are built up so as to guarantee conditions of both chemical and mechanical equilibrium between the two phases. If the overall conditions are of phase separation, it is expected that two phases will appear in different simulation boxes.
External links[edit]
Mixtures[edit]
Symmetric mixtures[edit]
Examples of symmetric mixtures can be found both in lattice of continuous model. The Ising model can be viewed as mixture of two different chemical species which de-mix at low temperature. The symmetry in the interactions can be exploited to simplify the calculation of phase diagrams.
See also[edit]
References[edit]
- ↑ Farid F. Abraham "Two-dimensional melting, solid-state stability, and the Kosterlitz-Thouless-Feynman criterion", Physical Review B 23 pp. 6145-6148 (1981)
- ↑ James R. Morris and Xueyu Song "The melting lines of model systems calculated from coexistence simulations", Journal of Chemical Physics 116 9352 (2002)
- ↑ Ramón García Fernández, José L. F. Abascal, and Carlos Vega "The melting point of ice Ih for common water models calculated from direct coexistence of the solid-liquid interface", Journal of Chemical Physics 124 144506 (2006)
- ↑ Athanassios Panagiotopoulos "Direct determination of phase coexistence properties of fluids by Monte Carlo simulation in a new ensemble", Molecular Physics 61 pp. 813-826 (1987)


















![{\displaystyle \left.P(V|N,p,T)\propto \exp \left[-{\frac {pV}{k_{B}T}}\right]\exp \left[-{\frac {A(N,V,T)}{k_{B}T}}\right]\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6ddfbd66fe2719734fbe09d0d9c3409ca5e8f4de)







![{\displaystyle \left.P(V|N,p_{eq},T)\simeq P_{v/l}\times \exp \left[-{\frac {\gamma (T){\mathcal {A}}}{k_{B}T}}\right]\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eaeb2b2c3df78961a87655f80d5a8d3e3e1784c8)






![{\displaystyle \left.P(V|N,p,T)\propto \exp \left[-{\frac {(p-p_{0})V}{k_{B}T}}\right]P_{0}(V|N,p_{0},T)\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/836ed28389208e606c4e9c43dfeb561e5366f081)














