Carnahan-Starling equation of state: Difference between revisions
No edit summary |
Carl McBride (talk | contribs) m (Slight tidy) |
||
| Line 18: | Line 18: | ||
*<math> \sigma </math> is the [[hard sphere model | hard sphere]] diameter. | *<math> \sigma </math> is the [[hard sphere model | hard sphere]] diameter. | ||
The | The Carnahan-Starling equation of state is not applicable for packing fractions greater than 0.55 <ref>[https://arxiv.org/abs/cond-mat/0605392 Hongqin Liu "A very accurate hard sphere equation of state over the entire stable and metstable region", arXiv:cond-mat/0605392 (2006)]</ref>. | ||
==Virial expansion== | ==Virial expansion== | ||
It is interesting to compare the [[Virial equation of state | virial coefficients]] of the Carnahan-Starling equation of state (Eq. 7 of <ref name="CH"> | It is interesting to compare the [[Virial equation of state | virial coefficients]] of the Carnahan-Starling equation of state (Eq. 7 of <ref name="CH"></ref>) with the [[Hard sphere: virial coefficients | hard sphere virial coefficients]] in three dimensions (exact up to <math>B_4</math>, and those of Clisby and McCoy <ref> [http://dx.doi.org/10.1007/s10955-005-8080-0 Nathan Clisby and Barry M. McCoy "Ninth and Tenth Order Virial Coefficients for Hard Spheres in D Dimensions", Journal of Statistical Physics '''122''' pp. 15-57 (2006)] </ref>): | ||
{| style="width:40%; height:100px" border="1" | {| style="width:40%; height:100px" border="1" | ||
|- | |- | ||
Revision as of 14:23, 18 June 2018
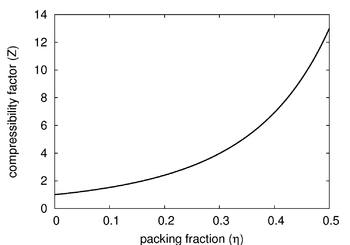
The Carnahan-Starling equation of state is an approximate (but quite good) equation of state for the fluid phase of the hard sphere model in three dimensions. It is given by (Ref [1] Eqn. 10).
where:
- is the compressibility factor
- is the pressure
- is the volume
- is the number of particles
- is the Boltzmann constant
- is the absolute temperature
- is the packing fraction:
- is the hard sphere diameter.
The Carnahan-Starling equation of state is not applicable for packing fractions greater than 0.55 [2].
Virial expansion
It is interesting to compare the virial coefficients of the Carnahan-Starling equation of state (Eq. 7 of [1]) with the hard sphere virial coefficients in three dimensions (exact up to , and those of Clisby and McCoy [3]):
| Clisby and McCoy | ||
| 2 | 4 | 4 |
| 3 | 10 | 10 |
| 4 | 18.3647684 | 18 |
| 5 | 28.224512 | 28 |
| 6 | 39.8151475 | 40 |
| 7 | 53.3444198 | 54 |
| 8 | 68.5375488 | 70 |
| 9 | 85.8128384 | 88 |
| 10 | 105.775104 | 108 |
Thermodynamic expressions
From the Carnahan-Starling equation for the fluid phase the following thermodynamic expressions can be derived (Ref [4] Eqs. 2.6, 2.7 and 2.8)
Pressure (compressibility):
Configurational chemical potential:
Isothermal compressibility:
where is the packing fraction.
Configurational Helmholtz energy function:
The 'Percus-Yevick' derivation
It is interesting to note (Ref [5] Eq. 6) that one can arrive at the Carnahan-Starling equation of state by adding two thirds of the exact solution of the Percus Yevick integral equation for hard spheres via the compressibility route, to one third via the pressure route, i.e.
The reason for this seems to be a slight mystery (see discussion in Ref. [6] ).
Kolafa correction
Jiri Kolafa produced a slight correction to the C-S EOS which results in improved accuracy [7]:
See also
References
- ↑ 1.0 1.1 N. F. Carnahan and K. E. Starling,"Equation of State for Nonattracting Rigid Spheres" Journal of Chemical Physics 51 pp. 635-636 (1969)
- ↑ Hongqin Liu "A very accurate hard sphere equation of state over the entire stable and metstable region", arXiv:cond-mat/0605392 (2006)
- ↑ Nathan Clisby and Barry M. McCoy "Ninth and Tenth Order Virial Coefficients for Hard Spheres in D Dimensions", Journal of Statistical Physics 122 pp. 15-57 (2006)
- ↑ Lloyd L. Lee "An accurate integral equation theory for hard spheres: Role of the zero-separation theorems in the closure relation", Journal of Chemical Physics 103 pp. 9388-9396 (1995)
- ↑ G. A. Mansoori, N. F. Carnahan, K. E. Starling, and T. W. Leland, Jr. "Equilibrium Thermodynamic Properties of the Mixture of Hard Spheres", Journal of Chemical Physics 54 pp. 1523-1525 (1971)
- ↑ Yuhua Song, E. A. Mason, and Richard M. Stratt "Why does the Carnahan-Starling equation work so well?", Journal of Physical Chemistry 93 pp. 6916-6919 (1989)
- ↑ Miguel Robles, Mariano López de Haro and Andrés Santos "Note: Equation of state and the freezing point in the hard-sphere model", Journal of Chemical Physics 140 136101 (2014)

















![{\displaystyle Z={\frac {pV}{Nk_{B}T}}={\frac {2}{3}}\left[{\frac {(1+\eta +\eta ^{2})}{(1-\eta )^{3}}}\right]+{\frac {1}{3}}\left[{\frac {(1+2\eta +3\eta ^{2})}{(1-\eta )^{2}}}\right]={\frac {1+\eta +\eta ^{2}-\eta ^{3}}{(1-\eta )^{3}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/be142b5b421225e5516478eb7d6d109e06d8dd61)
