Hard sphere model: Difference between revisions

Revision as of 14:37, 2 October 2008

The hard sphere intermolecular pair potential is defined as

\Phi _{12}\left(r\right)=\left\{{\begin{array}{lll}\infty &;&r<\sigma \\0&;&r\geq \sigma \end{array}}\right.

where $\Phi _{12}\left(r\right)$ is the intermolecular pair potential between two spheres at a distance $r:=|\mathbf {r} _{1}-\mathbf {r} _{2}|$ , and $\sigma$ is the diameter of the sphere. The hard sphere model can be considered to be a special case of the hard ellipsoid model, where each of the semi-axes has the same length, $a=b=c$ .

First simulations of hard spheres

The hard sphere model was one of the first ever systems studied:

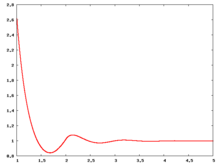
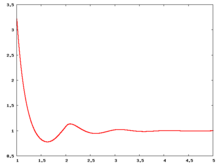
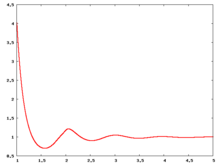
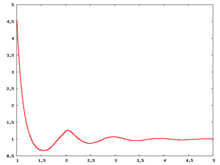
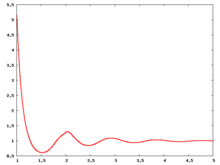
Radial distribution function

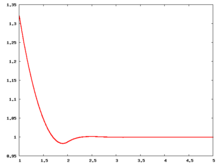
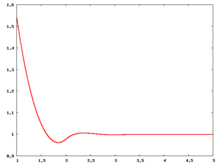
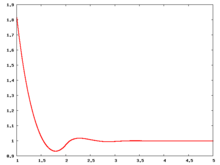
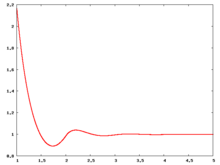
The following are a series of plots of the hard sphere radial distribution function (the total correlation function data was produced using the computer code written by Jiří Kolafa). The horizontal axis is in units of $\sigma$ where $\sigma$ is set to be 1. Click on image of interest to see a larger view.

$\rho =0.2$	$\rho =0.3$	$\rho =0.4$
$\rho =0.5$	$\rho =0.6$	$\rho =0.7$
$\rho =0.8$	$\rho =0.85$	$\rho =0.9$

The value of the radial distribution at contact, ${\mathrm {g} }(\sigma ^{+})$ , can be used to calculate the pressure via the equation of state (Ref 5 Eq. 1)

{\frac {p}{\rho k_{B}T}}=1+B_{2}\rho {\mathrm {g} }(\sigma ^{+})

where the second virial coefficient, $B_{2}$ , is given by

B_{2}={\frac {2\pi }{3}}\sigma ^{3}

.

Carnahan and Starling (Ref. 6) provided the following expression for ${\mathrm {g} }(\sigma ^{+})$ (Ref. 5 Eq. 3)

{\mathrm {g} }(\sigma ^{+})={\frac {1-\eta /2}{(1-\eta )^{3}}}

where $\eta$ is the packing fraction.

Over the years many groups have studied the radial distribution function of the hard sphere model:

Direct correlation function

For the direct correlation function see:

C. F. Tejero and M. López De Haro "Direct correlation function of the hard-sphere fluid", Molecular Physics 105 pp. 2999-3004 (2007)

Fluid-solid transition

The hard sphere system undergoes a fluid-solid first order transition (Ref. 1). The fluid-solid coexistence densities ( $\rho ^{*}=\rho \sigma ^{3}$ ) are given by

$\rho _{\mathrm {solid} }^{*}$	$\rho _{\mathrm {liquid} }^{*}$	Reference
1.041	0.945	Ref. 1
1.0376	0.9391	Ref. 2
1.0367(10)	0.9387(10)	Ref. 3
1.0372	0.9387	Ref. 4
1.0369(33)	0.9375(14)	Ref. 5
1.037	0.938	Ref. 6

The coexistence pressure is given by

$p(k_{B}T/\sigma ^{3})$	Reference
11.567	Ref. 2
11.57(10)	Ref. 3
11.54(4)	Ref. 5
11.50(9)	Ref. 7
11.55(11)	Ref. 8

Solid structure

The Kepler conjecture states that the optimal packing for three dimensional spheres is either cubic or hexagonal close packing, both of which have maximum densities of $\pi /(3{\sqrt {2}})\approx 74.048\%$ . However, for hard spheres at close packing the face centred cubic phase is the more stable (Ref. 3).

Equations of state

Main article: Equations of state for hard spheres

Virial coefficients

Main article: Hard sphere: virial coefficients

Experimental results

Pusey and van Megen used a suspension of PMMA particles of radius 305 $\pm$ 10 nm, suspended in poly-12-hydroxystearic acid:

P. N. Pusey and W. van Megen "Phase behaviour of concentrated suspensions of nearly hard colloidal spheres", Nature 320 pp. 340 - 342 (1986)

For results obtained from the Colloidal Disorder - Order Transition (CDOT) experiments performed on-board the Space Shuttles Columbia and Discovery see Ref. 3.

External links

Hard disks and spheres computer code on SMAC-wiki.

Related systems

Hard spheres in other dimensions

1-dimensional case: hard rods.
2-dimensional case: hard disks.
Hard hyperspheres

References

@@ Line 94: / Line 94: @@
 ==Solid structure==
-The [http://mathworld.wolfram.com/KeplerConjecture.html Kepler conjecture] states that the optimal packing for hard spheres is either cubic or hexagonal close [[Lattice Structures | packing]], both of which have maximum densities of <math>\pi/(3 \sqrt{2}) \approx 74.048%</math>.
+The [http://mathworld.wolfram.com/KeplerConjecture.html Kepler conjecture] states that the optimal packing for three dimensional spheres is either cubic or hexagonal close [[Lattice Structures | packing]], both of which have maximum densities of <math>\pi/(3 \sqrt{2}) \approx 74.048%</math>. However, for hard spheres at close packing the [[Building up a face centered cubic lattice |face centred cubic]] phase is the more stable (Ref. 3).
-*[http://dx.doi.org/10.1038/26609 Neil J. A. Sloane "Kepler's conjecture confirmed", Nature '''395''' pp. 435-436 (1998)]
+#[http://dx.doi.org/10.1038/26609 Neil J. A. Sloane "Kepler's conjecture confirmed", Nature '''395''' pp. 435-436 (1998)]
-*[http://dx.doi.org/10.1039/a701761h Leslie V. Woodcock "Computation of the free energy for alternative crystal structures of hard spheres", Faraday Discussions '''106''' pp. 325 - 338 (1997)]
+#[http://dx.doi.org/10.1103/PhysRevE.52.3632 C. F. Tejero, M. S. Ripoll, and A. Pérez "Pressure of the hard-sphere solid", Physical Review E  '''52''' pp. 3632-3636 (1995)]
-*[http://dx.doi.org/10.1103/PhysRevE.52.3632 C. F. Tejero, M. S. Ripoll, and A. Pérez "Pressure of the hard-sphere solid", Physical Review E  '''52''' pp. 3632-3636 (1995)]
+#[http://dx.doi.org/10.1039/a701761h Leslie V. Woodcock "Computation of the free energy for alternative crystal structures of hard spheres", Faraday Discussions '''106''' pp. 325 - 338 (1997)]
 == Equations of state ==

Hard sphere model: Difference between revisions

Revision as of 14:37, 2 October 2008

Contents

First simulations of hard spheres

Radial distribution function

Direct correlation function

Fluid-solid transition

Solid structure

Equations of state

Virial coefficients

Experimental results

External links

Related systems

Hard spheres in other dimensions

References

Navigation menu

Hard sphere model: Difference between revisions

Revision as of 14:37, 2 October 2008

First simulations of hard spheres

Radial distribution function

Direct correlation function

Fluid-solid transition

Solid structure

Equations of state

Virial coefficients

Experimental results

External links

Related systems

Hard spheres in other dimensions

References

Navigation menu

Search