Lennard-Jones model

The Lennard-Jones intermolecular pair potential was developed by Sir John Edward Lennard-Jones in 1931 (Ref. 1).

Functional form

The Lennard-Jones potential is given by:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi(r) = 4 \epsilon \left[ \left(\frac{\sigma}{r} \right)^{12}- \left( \frac{\sigma}{r}\right)^6 \right] }

where:

• Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi(r) } is the intermolecular pair potential between two particles at a distance r;

• Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma }  : diameter (length);

• Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon }  : well depth (energy)

Reduced units:

• Density, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho^* \equiv \rho \sigma^3 } , where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho = N/V } (number of particles Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N } divided by the volume $V$.)

• Temperature; Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T^* \equiv k_B T/\epsilon } , where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T } is the absolute temperature and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_B } is the Boltzmann constant

Argon

The Lennard-Jones parameters for argon are Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon/k_B \approx} 119.8 K and $\sigma \approx$ 0.3405 nm. (Ref. ?)

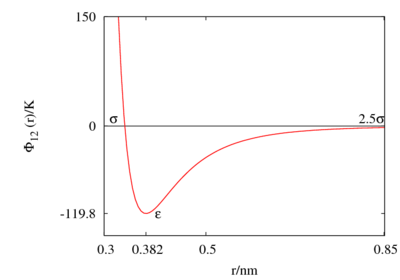
This figure was produced using gnuplot with the command:

plot (4*120*((0.34/x)**12-(0.34/x)**6))

Features

Special points:

• Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi(\sigma) = 0 }
• Minimum value of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi(r) } at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r = r_{min} } ;

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{r_{min}}{\sigma} = 2^{1/6} \simeq 1.12246 ... }

Critical point

The location of the critical point is (Caillol (Ref. 3))

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_c^* = 1.326 \pm 0.002}

at a reduced density of

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho_c^* = 0.316 \pm 0.002} .

Triple point

The location of the triple point as found by Mastny and de Pablo (Ref. 2) is

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_{tp}^* = 0.694}

Approximations in simulation: truncation and shifting

The Lennard-Jones model is often used with a cutoff radius of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2.5 \sigma} . See Mastny and de Pablo (Ref. 2) for an analysis of the effect of this cutoff on the melting line.

m-n Lennard-Jones potential

It is relatively common to encounter potential functions given by:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi (r) = c_{m,n} \epsilon \left[ \left( \frac{ \sigma }{r } \right)^m - \left( \frac{\sigma}{r} \right)^n \right]. }

with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m } and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n } being positive integers and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m > n } . Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c_{m,n} } is chosen such that the minimum value of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi(r) } being Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi_{min} = - \epsilon } . Such forms are usually referred to as m-n Lennard-Jones Potential. For example, the 9-3 Lennard-Jones interaction potential is often used to model the interaction between the atoms/molecules of a fluid and a continuous solid wall. On the '9-3 Lennard-Jones potential' page a justification of this use is presented.

Related pages

• Phase diagram of the Lennard-Jones model
• Lennard-Jones model: virial coefficients
• Lennard-Jones equation of state
• Lennard-Jones sticks
• Lennard-Jones disks
• 9-3 Lennard-Jones potential

References

1. J. E. Lennard-Jones, "Cohesion", Proceedings of the Physical Society, 43 pp. 461-482 (1931)
2. Ethan A. Mastny and Juan J. de Pablo "Melting line of the Lennard-Jones system, infinite size, and full potential", Journal of Chemical Physics 127 104504 (2007)
3. J. M. Caillol " Critical-point of the Lennard-Jones fluid: A finite-size scaling study", Journal of Chemical Physics 109 pp. 4885-4893 (1998)