Hard sphere model: Difference between revisions

From SklogWiki
Jump to navigation Jump to search
m (Added mention of rigid sphere model in older papers)
(→‎Fluid-solid transition: include Kirkwood-Alder transition nomenclature)
Line 48: Line 48:
<ref>[http://dx.doi.org/10.1063/1.2201699 M. López de Haro, A. Santos and S. B. Yuste "On the radial distribution function of a hard-sphere fluid",  Journal of Chemical Physics '''124'''  236102 (2006)]</ref>
<ref>[http://dx.doi.org/10.1063/1.2201699 M. López de Haro, A. Santos and S. B. Yuste "On the radial distribution function of a hard-sphere fluid",  Journal of Chemical Physics '''124'''  236102 (2006)]</ref>
==Fluid-solid transition==
==Fluid-solid transition==
The hard sphere system undergoes a [[Solid-liquid phase transitions |fluid-solid]] [[First-order transitions |first order transition]] <ref name="HooverRee">[http://dx.doi.org/10.1063/1.1670641    William G. Hoover and Francis H. Ree "Melting Transition and Communal Entropy for Hard Spheres", Journal of Chemical Physics '''49''' pp. 3609-3617  (1968)]</ref>
The hard sphere system undergoes a [[Solid-liquid phase transitions |fluid-solid]] [[First-order transitions |first order transition]] <ref name="HooverRee">[http://dx.doi.org/10.1063/1.1670641    William G. Hoover and Francis H. Ree "Melting Transition and Communal Entropy for Hard Spheres", Journal of Chemical Physics '''49''' pp. 3609-3617  (1968)]</ref>, now referred as the Kirkwood-Alder transition <ref name="GastRussel">[http://dx.doi.org/10.1063/1.882495 Alice P. Gast and William B. Russel
      "Simple Ordering in Complex Fluids", Physics Today '''51''' (12) pp. 24-30  (1998)]</ref>.
The fluid-solid coexistence densities (<math>\rho^* = \rho \sigma^3</math>) are given by
The fluid-solid coexistence densities (<math>\rho^* = \rho \sigma^3</math>) are given by
:{| border="1"
:{| border="1"
Line 99: Line 100:
| 4.887(3) || 3.719(8) || <ref name="Miguel"> </ref>
| 4.887(3) || 3.719(8) || <ref name="Miguel"> </ref>
|}
|}
==Helmholtz energy function==
==Helmholtz energy function==
Values for the [[Helmholtz energy function]] (<math>A</math>) are given in the following Table:
Values for the [[Helmholtz energy function]] (<math>A</math>) are given in the following Table:

Revision as of 22:09, 26 August 2010

The hard sphere model (sometimes known as the rigid sphere model) is defined as

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi_{12}\left(r \right) } is the intermolecular pair potential between two spheres at a distance Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r := |\mathbf{r}_1 - \mathbf{r}_2|} , and is the diameter of the sphere. The hard sphere model can be considered to be a special case of the hard ellipsoid model, where each of the semi-axes has the same length, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a=b=c} .

First simulations of hard spheres

The hard sphere model, along with its two-dimensional manifestation hard disks, was one of the first ever systems studied using computer simulation techniques with a view to understanding the thermodynamics of the fluid and solid phases and their corresponding phase transition [1] [2] [3]

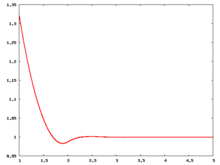
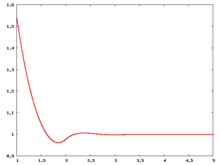
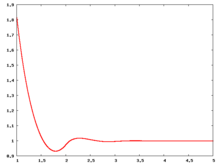
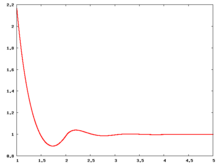
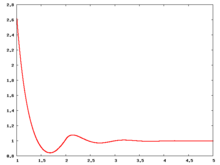
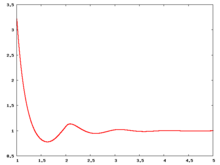
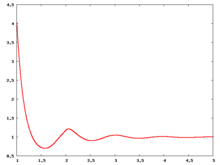
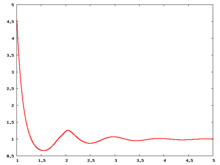
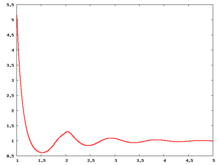
Fluid phase radial distribution function

The following are a series of plots of the hard sphere radial distribution function [4]. The horizontal axis is in units of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma} where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma} is set to be 1. Click on image of interest to see a larger view.

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho=0.2}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho=0.3}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho=0.4}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho=0.5}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho=0.6}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho=0.7}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho=0.8}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho=0.85}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho=0.9}

The value of the radial distribution at contact, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\mathrm g}(\sigma^+)} , can be used to calculate the pressure via the equation of state (Eq. 1 in [5])

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{p}{\rho k_BT}= 1 + B_2 \rho {\mathrm g}(\sigma^+)}

where the second virial coefficient, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B_2} , is given by

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B_2 = \frac{2\pi}{3}\sigma^3} .

Carnahan and Starling [6] provided the following expression for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\mathrm g}(\sigma^+)} (Eq. 3 in [5])

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\mathrm g}(\sigma^+)= \frac{1-\eta/2}{(1-\eta)^3}}

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \eta} is the packing fraction.

Over the years many groups have studied the radial distribution function of the hard sphere model: [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17]

Fluid-solid transition

The hard sphere system undergoes a fluid-solid first order transition [18], now referred as the Kirkwood-Alder transition [19]. The fluid-solid coexistence densities (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho^* = \rho \sigma^3} ) are given by

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho^*_{\mathrm {solid}}} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho^*_{\mathrm {fluid}}} Reference
1.041 0.945 [18]
1.0376 0.9391 [20]
1.0367(10) 0.9387(10) [21]
1.0372 0.9387 [22]
1.0369(33) 0.9375(14) [23]
1.037 0.938 [24]
1.035(3) 0.936(2) [25]

The coexistence pressure is given by

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p (k_BT/\sigma^3) } Reference
11.567 [20]
11.57(10) [21]
11.54(4) [23]
11.50(9) [26]
11.55(11) [27]
11.48(11) [25]

The coexistence chemical potential is given by

Reference
15.980(11) [25]

The Helmholtz energy function (in units of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Nk_BT} ) is given by

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A_{\mathrm {solid}}} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A_{\mathrm {fluid}}} Reference
4.887(3) 3.719(8) [25]

Helmholtz energy function

Values for the Helmholtz energy function (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} ) are given in the following Table:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A/(Nk_BT)} Reference
0.25 0.620 Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pm} 0.002 Table I [28]
0.50 1.541 Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pm} 0.002 Table I [28]
0.75 3.009 Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pm} 0.002 Table I [28]
1.04086 4.959 Table VI [22]
1.099975 5.631 Table VI [22]
1.150000 6.274 Table VI [22]

Solid structure

The Kepler conjecture states that the optimal packing for three dimensional spheres is either cubic or hexagonal close packing, both of which have maximum densities of [29] [30]. However, for hard spheres at close packing the face centred cubic phase is the more stable [31]

Direct correlation function

For the direct correlation function see: [32] [33]

Bridge function

Details of the bridge function for hard sphere can be found in the following publication [34]

Equations of state

Main article: Equations of state for hard spheres

Virial coefficients

Main article: Hard sphere: virial coefficients

Experimental results

Pusey and van Megen used a suspension of PMMA particles of radius 305 Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pm} 10 nm, suspended in poly-12-hydroxystearic acid [35] For results obtained from the Colloidal Disorder - Order Transition (CDOT) experiments performed on-board the Space Shuttles Columbia and Discovery see Ref. [36]

Mixtures

Related systems

Hard spheres in other dimensions:

References

  1. ↑ Marshall N. Rosenbluth and Arianna W. Rosenbluth "Further Results on Monte Carlo Equations of State", Journal of Chemical Physics 22 pp. 881-884 (1954)
  2. ↑ W. W. Wood and J. D. Jacobson "Preliminary Results from a Recalculation of the Monte Carlo Equation of State of Hard Spheres", Journal of Chemical Physics 27 pp. 1207-1208 (1957)
  3. ↑ B. J. Alder and T. E. Wainwright "Phase Transition for a Hard Sphere System", Journal of Chemical Physics 27 pp. 1208-1209 (1957)
  4. ↑ The total correlation function data was produced using the computer code written by Jiří Kolafa
  5. ↑ 5.0 5.1 Fu-Ming Tao, Yuhua Song, and E. A. Mason "Derivative of the hard-sphere radial distribution function at contact", Physical Review A 46 pp. 8007-8008 (1992)
  6. ↑ N. F.Carnahan and K. E.Starling,"Equation of State for Nonattracting Rigid Spheres" Journal of Chemical Physics 51 pp. 635-636 (1969)
  7. ↑ John G. Kirkwood, Eugene K. Maun, and Berni J. Alder "Radial Distribution Functions and the Equation of State of a Fluid Composed of Rigid Spherical Molecules", Journal of Chemical Physics 18 pp. 1040- (1950)
  8. ↑ B. R. A. Nijboer and L. Van Hove "Radial Distribution Function of a Gas of Hard Spheres and the Superposition Approximation", Physical Review 85 pp. 777 - 783 (1952)
  9. ↑ B. J. Alder, S. P. Frankel, and V. A. Lewinson "Radial Distribution Function Calculated by the Monte-Carlo Method for a Hard Sphere Fluid", Journal of Chemical Physics 23 pp. 417- (1955)
  10. ↑ Francis H. Ree, R. Norris Keeler, and Shaun L. McCarthy "Radial Distribution Function of Hard Spheres", Journal of Chemical Physics 44 pp. 3407- (1966)
  11. ↑ W. R. Smith and D. Henderson "Analytical representation of the Percus-Yevick hard-sphere radial distribution function", Molecular Physics 19 pp. 411-415 (1970)
  12. ↑ J. A. Barker and D. Henderson "Monte Carlo values for the radial distribution function of a system of fluid hard spheres", Molecular Physics 21 pp. 187-191 (1971)
  13. ↑ J. M. Kincaid and J. J. Weis "Radial distribution function of a hard-sphere solid", Molecular Physics 34 pp. 931-938 (1977)
  14. ↑ S. Bravo Yuste and A. Santos "Radial distribution function for hard spheres", Physical Review A 43 pp. 5418-5423 (1991)
  15. ↑ Jaeeon Chang and Stanley I. Sandler "A real function representation for the structure of the hard-sphere fluid", Molecular Physics 81 pp. 735-744 (1994)
  16. ↑ Andrij Trokhymchuk, Ivo Nezbeda and Jan Jirsák "Hard-sphere radial distribution function again", Journal of Chemical Physics 123 024501 (2005)
  17. ↑ M. López de Haro, A. Santos and S. B. Yuste "On the radial distribution function of a hard-sphere fluid", Journal of Chemical Physics 124 236102 (2006)
  18. ↑ 18.0 18.1 William G. Hoover and Francis H. Ree "Melting Transition and Communal Entropy for Hard Spheres", Journal of Chemical Physics 49 pp. 3609-3617 (1968)
  19. ↑ [http://dx.doi.org/10.1063/1.882495 Alice P. Gast and William B. Russel "Simple Ordering in Complex Fluids", Physics Today 51 (12) pp. 24-30 (1998)]
  20. ↑ 20.0 20.1 Daan Frenkel and Berend Smit "Understanding Molecular Simulation: From Algorithms to Applications", Second Edition (2002) (ISBN 0-12-267351-4) p. 261.
  21. ↑ 21.0 21.1 Andrea Fortini and Marjolein Dijkstra "Phase behaviour of hard spheres confined between parallel hard plates: manipulation of colloidal crystal structures by confinement", Journal of Physics: Condensed Matter 18 pp. L371-L378 (2006)
  22. ↑ 22.0 22.1 22.2 22.3 Carlos Vega and Eva G. Noya "Revisiting the Frenkel-Ladd method to compute the free energy of solids: The Einstein molecule approach", Journal of Chemical Physics 127 154113 (2007)
  23. ↑ 23.0 23.1 Eva G. Noya, Carlos Vega, and Enrique de Miguel "Determination of the melting point of hard spheres from direct coexistence simulation methods", Journal of Chemical Physics 128 154507 (2008)
  24. ↑ Ruslan L. Davidchack and Brian B. Laird "Simulation of the hard-sphere crystal–melt interface", Journal of Chemical Physics 108 pp. 9452-9462 (1998)
  25. ↑ 25.0 25.1 25.2 25.3 Enrique de Miguel "Estimating errors in free energy calculations from thermodynamic integration using fitted data", Journal of Chemical Physics 129 214112 (2008)
  26. ↑ N. B. Wilding and A. D. Bruce "Freezing by Monte Carlo Phase Switch", Physical Review Letters 85 pp. 5138-5141 (2000)
  27. ↑ Robin J. Speedy "Pressure of the metastable hard-sphere fluid", Journal of Physics: Condensed Matter 9 pp. 8591-8599 (1997)
  28. ↑ 28.0 28.1 28.2 T. Schilling and F. Schmid "Computing absolute free energies of disordered structures by molecular simulation", Journal of Chemical Physics 131 231102 (2009)
  29. ↑ Neil J. A. Sloane "Kepler's conjecture confirmed", Nature 395 pp. 435-436 (1998)
  30. ↑ C. F. Tejero, M. S. Ripoll, and A. Pérez "Pressure of the hard-sphere solid", Physical Review E 52 pp. 3632-3636 (1995)
  31. ↑ Leslie V. Woodcock "Computation of the free energy for alternative crystal structures of hard spheres", Faraday Discussions 106 pp. 325 - 338 (1997)
  32. ↑ C. F. Tejero and M. López De Haro "Direct correlation function of the hard-sphere fluid", Molecular Physics 105 pp. 2999-3004 (2007)
  33. ↑ Matthew Dennison, Andrew J. Masters, David L. Cheung, and Michael P. Allen "Calculation of direct correlation function for hard particles using a virial expansion", Molecular Physics pp. 375-382 (2009)
  34. ↑ Jiri Kolafa, Stanislav Labik and Anatol Malijevsky "The bridge function of hard spheres by direct inversion of computer simulation data", Molecular Physics 100 pp. 2629-2640 (2002)
  35. ↑ P. N. Pusey and W. van Megen "Phase behaviour of concentrated suspensions of nearly hard colloidal spheres", Nature 320 pp. 340-342 (1986)
  36. ↑ Z. Chenga, P. M. Chaikina, W. B. Russelb, W. V. Meyerc, J. Zhub, R. B. Rogersc and R. H. Ottewilld, "Phase diagram of hard spheres", Materials & Design 22 pp. 529-534 (2001)

Related reading

External links

Retrieved from "http://www.sklogwiki.org/SklogWiki/index.php?title=Hard_sphere_model&oldid=10523"