Anisotropic particles with tetrahedral symmetry
Anisotropic particles with tetrahedral symmetry
Kern and Frenkel model[edit]
Phase diagram[edit]
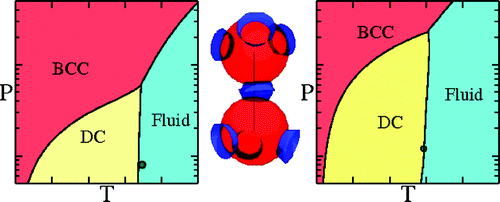
The phase diagram of the tetrahedral Kern and Frenkel patchy model exhibits the following solid phases[1][2]: diamond crystal (DC), body centred cubic (BCC) and face centred cubic (FCC). The gas-liquid critical point becomes metastable with respect to the diamond crystal when the range of the interaction becomes short (roughly less than 15% of the diameter).
In contrast to isotropic models, the critical point becomes only weakly metastable with respect to the solid as the interaction range narrows (from left to right in the figure).
Crystallization[edit]
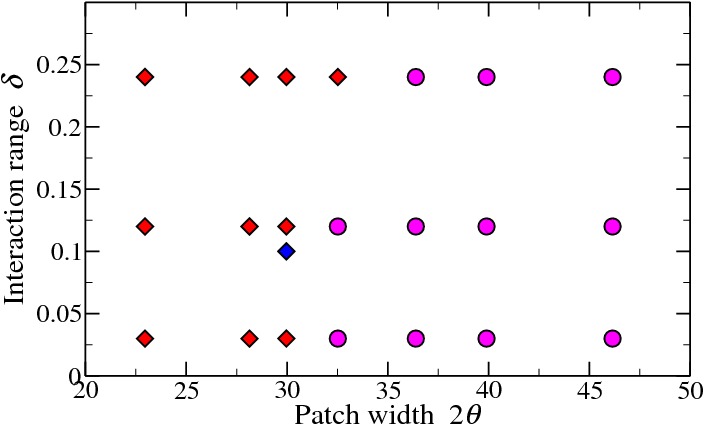
Tetrahedral Kern-Frenkel patchy particles crystallise spontaneously into open tetrahedral networks for narrow patches (solid angle < 30). The interaction range does not play an important role in crystallisation [3]
Interaction range, , versus patch angular width. Diamonds correspond to crystallising and circles to glass–forming models. The point studied in Ref. [4] is included.
When the patches in this model are made even wider (while still enforcing the limit of a single bond per patch), the diamond phase becomes metastable with respect to a liquid phase, which is stable even in the zero-temperature limit [5].
Modulated patchy Lennard-Jones model[edit]
The solid phases of the modulated patchy Lennard-Jones model has also been studied [6]
Lattice model[edit]
See also[edit]
References[edit]
- ↑ Flavio Romano, Eduardo Sanz and Francesco Sciortino "Role of the Range in the Fluid−Crystal Coexistence for a Patchy Particle Model", Journal of Physical Chemistry B 113 pp. 15133–15136 (2009)
- ↑ Flavio Romano, Eduardo Sanz and Francesco Sciortino "Phase diagram of a tetrahedral patchy particle model for different interaction ranges", Journal of Chemical Physics 132 184501 (2010)
- ↑ Flavio Romano, Eduardo Sanz, and Francesco Sciortino "Crystallization of tetrahedral patchy particles in silico", Journal of Chemical Physics 134 174502 (2011)
- ↑ Zhenli Zhang, Aaron S. Keys, Ting Chen, and Sharon C. Glotzer "Self-Assembly of Patchy Particles into Diamond Structures through Molecular Mimicry", Langmuir 21 11547 (2005)
- ↑ Frank Smallenburg and Francesco Sciortino "Liquids more stable than crystals in particles with limited valence and flexible bonds", Nature Physics 9 554 (2013)
- ↑ Eva G. Noya, Carlos Vega, Jonathan P. K. Doye, and Ard A. Louis "The stability of a crystal with diamond structure for patchy particles with tetrahedral symmetry", Journal of Chemical Physics 132 234511 (2010)
- ↑ N. G. Almarza and E. G. Noya "Phase transitions of a lattice model for patchy particles with tetrahedral symmetry", Molecular Physics 109 pp. 65-74 (2011)
- Related reading
- G. Munaó, D. Costa, F. Sciortino, and C. Caccamo "Simulation and theory of a model for tetrahedral colloidal particles", Journal of Chemical Physics 134 194502 (2011)
- Ivan Saika-Voivod, Frank Smallenburg and Francesco Sciortino "Understanding tetrahedral liquids through patchy colloids", Journal of Chemical Physics 139 234901 (2013)