Critical points: Difference between revisions

From SklogWiki
Jump to navigation Jump to search
m (Added a reference.)
m (Anoterh reference)
Line 1: Line 1:
[[Image:press_temp.png|thumb|right]]
[[Image:press_temp.png|thumb|right]]
The '''critical point''', discovered in 1822 by Charles Cagniard de la Tour <ref>Charles Cagniard de la Tour "", Annales de chimie et de physique '''21''' pp. 127- (1822)</ref>, is a point found at the end of the liquid-vapour coexistence curve (the red point shown on the [[pressure-temperature]] plot on the right). At this point the [[temperature]] is known as the ''critical temperature'' <math>(T_c)</math>
The '''critical point''', discovered in 1822 by Charles Cagniard de la Tour <ref>Charles Cagniard de la Tour "Exposé de quelques résultats obtenu par l'action combinée de la chaleur et de la compression sur certains liquides, tels que l'eau, l'alcool, l'éther sulfurique et l'essence de pétrole rectifiée", Annales de chimie et de physique '''21''' pp. 127-132 (1822)</ref><ref>[http://dx.doi.org/10.1590/S1806-11172009000200015 Bertrand Berche, Malte Henkel, and Ralph Kenna "Critical phenomena: 150 years since Cagniard de la Tour", Revista Brasileira de Ensino de Física '''31''' pp.2602.1-2602.4 (2009)] (in English [http://arxiv.org/abs/0905.1886v1 arXiv:0905.1886v1])</ref> , is a point found at the end of the liquid-vapour coexistence curve (the red point shown on the [[pressure-temperature]] plot on the right). At this point the [[temperature]] is known as the ''critical temperature'' <math>(T_c)</math>
and the [[pressure]] is known as the ''critical pressure'' <math>(P_c)</math>.
and the [[pressure]] is known as the ''critical pressure'' <math>(P_c)</math>.
For an interesting discourse on the "discovery" of the liquid-vapour critical point, the  Bakerian Lecture of [[Thomas Andrews]]
For an interesting discourse on the "discovery" of the liquid-vapour critical point, the  Bakerian Lecture of [[Thomas Andrews]]

Revision as of 16:29, 20 November 2009

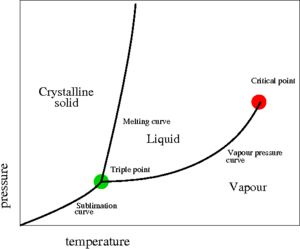
The critical point, discovered in 1822 by Charles Cagniard de la Tour [1][2] , is a point found at the end of the liquid-vapour coexistence curve (the red point shown on the pressure-temperature plot on the right). At this point the temperature is known as the critical temperature Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (T_c)} and the pressure is known as the critical pressure Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (P_c)} . For an interesting discourse on the "discovery" of the liquid-vapour critical point, the Bakerian Lecture of Thomas Andrews makes good reading [3]. Critical points are singularities in the partition function. In the critical point vicinity (Ref. [4] Eq. 17a)

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left.\frac{\partial P}{\partial n}\right\vert_{T} \simeq 0}

and

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n \int_0^{\infty} c(r) ~4 \pi r^2 ~{\rm d}r \simeq 1}

For a review of the critical region see the work of Michael E. Fisher [5]

"... Turning now to the question of specific heats, it has long been known that real gases exhibit a large ``anomalous" specific-heat maximum above Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_c} which lies near the critical isochore and which is not expected on classical theory..."

also

"... measurements (Ref. [6] ) of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_V(T)} for argon along the critical isochore suggest strongly that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_V(T) \rightarrow \infty ~{\rm as} ~ T \rightarrow T_c \pm} . Such a result is again inconsistent with classical theory."

Thus in the vicinity of the liquid-vapour critical point, both the isothermal compressibility and the heat capacity at constant pressure diverge to infinity.

Liquid-liquid critical point

Solid-liquid critical point

It is widely held that there is no solid-liquid critical point. The reasoning behind this was given on the grounds of symmetry by Landau and Lifshitz [7]. However, recent work using the Z2 potential suggests that this may not be the last word on the subject. [8].

Tricritical points

Critical exponents

Main article: Critical exponents

See also

References

  1. ↑ Charles Cagniard de la Tour "Exposé de quelques résultats obtenu par l'action combinée de la chaleur et de la compression sur certains liquides, tels que l'eau, l'alcool, l'éther sulfurique et l'essence de pétrole rectifiée", Annales de chimie et de physique 21 pp. 127-132 (1822)
  2. ↑ Bertrand Berche, Malte Henkel, and Ralph Kenna "Critical phenomena: 150 years since Cagniard de la Tour", Revista Brasileira de Ensino de Física 31 pp.2602.1-2602.4 (2009) (in English arXiv:0905.1886v1)
  3. ↑ Thomas Andrews "The Bakerian Lecture: On the Continuity of the Gaseous and Liquid States of Matter", Philosophical Transactions of the Royal Society of London 159 pp. 575-590 (1869)
  4. ↑ G. A. Martynov; G. N. Sarkisov "Exact equations and the theory of liquids. V", Molecular Physics 49 pp. 1495-1504 (1983)
  5. ↑ Michael E. Fisher "Correlation Functions and the Critical Region of Simple Fluids", Journal of Mathematical Physics 5 pp. 944-962 (1964)
  6. ↑ A. Michels, J.M. Levelt and G.J. Wolkers "Thermodynamic properties of argon at temperatures between 0°C and −140°C and at densities up to 640 amagat (pressures up to 1050 atm.)", Physica 24 pp. 769-794 (1958)
  7. ↑ L. D. Landau and E. M. Lifshitz, "Statistical Physics" (Course of Theoretical Physics, Volume 5) 3rd Edition Part 1, Chapter XIV, Pergamon Press (1980) § 83 p. 258
  8. ↑ Måns Elenius and Mikhail Dzugutov "Evidence for a liquid-solid critical point in a simple monatomic system", Journal of Chemical Physics 131, 104502 (2009)

Related reading

Retrieved from "http://www.sklogwiki.org/SklogWiki/index.php?title=Critical_points&oldid=9325"