Lennard-Jones model

The Lennard-Jones potential was developed by Sir John Edward Lennard-Jones.

Lennard-Jones potential

The Lennard-Jones potential is given by:

$\Phi (r)=4\epsilon \left[\left({\frac {\sigma }{r}}\right)^{12}-\left({\frac {\sigma }{r}}\right)^{6}\right]$

where:

• $\Phi (r)$ is the intermolecular pair potential between two particles at a distance r;

• $\sigma$ : diameter (length);

• $\epsilon$ : well depth (energy)

Reduced units:

• Density, $\rho ^{*}\equiv \rho \sigma ^{3}$, where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho = N/V } (number of particles Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N } divided by the volume Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V } .)

• Temperature; Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T^* \equiv k_B T/\epsilon } , where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T } is the absolute temperature and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_B } is the Boltzmann constant

Argon

The Lennard-Jones parameters for argon are Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon/k_B \approx} 119.8 K and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma \approx} 0.3405 nm. (Ref. ?)

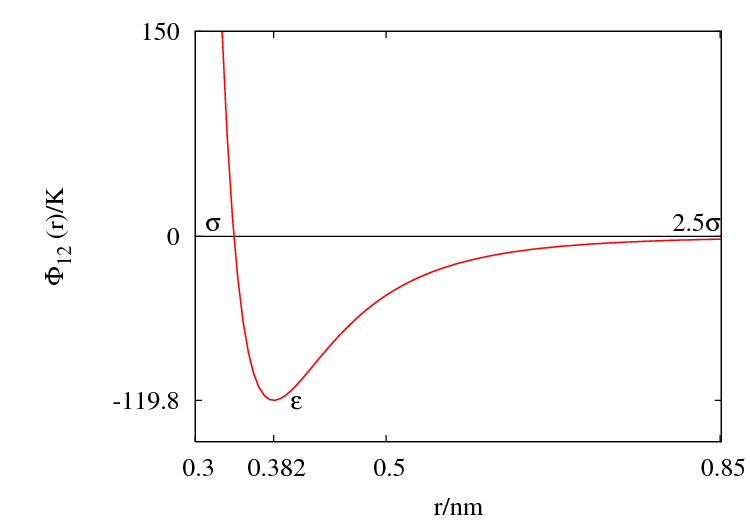
This figure was produced using gnuplot with the command:

plot (4*120*((0.34/x)**12-(0.34/x)**6))

Features

Special points:

• Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi(\sigma) = 0 }

• Minimum value of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi(r) } at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r = r_{min} } ;

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{r_{min}}{\sigma} = 2^{1/6} \simeq 1.12246 ... }

Tripple point

The location of the triple point as found by Mastny and de Pablo (Ref. 2) is

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_{tp}^* = 0.694}

Approximations in simulation: truncation and shifting

The Lennard-Jones model is often used with a cutoff radius of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2.5 \sigma} . See Mastny and de Pablo (Ref. 2) fa an analysis of the effect of this cutoff on the melting line.

Related potential models

It is relatively common the use of potential functions given by:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi (r) = c_{m,n} \epsilon \left[ \left( \frac{ \sigma }{r } \right)^m - \left( \frac{\sigma}{r} \right)^n \right]. }

with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m } and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n } being positive integer numbers and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m > n } , and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c_{m,n} } is chosen to get the minimum value of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi(r) } being Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi_{min} = - \epsilon }

These forms are usually referred to as m-n Lennard-Jones Potential.

The 9-3 Lennard-Jones interaction potential is often use to model the interaction between the atoms/molecules of a fluid and a continuous solid wall. In (9-3 Lennard-Jones potential) a justification of this use is presented.

Other dimensions

• 1-dimensional case: Lennard-Jones rods.
• 2-dimensional case: Lennard-Jones disks.

See also

• Phase diagram of the Lennard-Jones model
• Lennard-Jones model: virial coefficients
• Lennard-Jones equation of state

References

1. J. E. Lennard-Jones, "Cohesion", Proceedings of the Physical Society, 43 pp. 461-482 (1931)
2. Ethan A. Mastny and Juan J. de Pablo "Melting line of the Lennard-Jones system, infinite size, and full potential", Journal of Chemical Physics 127 104504 (2007)