Van der Waals equation of state

The van der Waals equation of state, developed by Johannes Diderik van der Waals, can be written as

$\left.p={\frac {nRT}{V-nb}}-a\left({\frac {n}{V}}\right)^{2}\right.$.

where:

• Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p } is the pressure,

• Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V } is the volume,

• Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n } is the number of moles,

• Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T } is the absolute temperature,

• $R$ is the so-called gas constant; Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R = N_A k_B } , with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N_A } being the Avogadro constant and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_B} being the Boltzmann constant.

The van der Waals equation of state takes into account two features that are absent in the ideal Gas equation of state: The parameter Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b } introduces somehow the repulsive behavior between pairs of molecules at short distances, it represents the minimum molar volume of the system, whereas $a$ measures the attractive interactions between the molecules. The van der Waals equation of state leads to a liquid-vapor equilibrium at low temperatures, with the corresponding critical point.

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a= \frac{27}{64}\frac{R^2T_c^2}{P_c}}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b= \frac{RT_c}{8P_c}}

Critical point

The critical point for the van der Waals equation of state can be found at

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_c= \frac{8a}{27bR}} ,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p_c=\frac{a}{27b^2}}

and at

$\left.v_{c}\right.=3b$.

Dimensionless formulation

If one takes the following quantities

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tilde{p} = \frac{p}{p_c};~ \tilde{v} = \frac{v}{v_c}; ~\tilde{t} = \frac{T}{T_c};}

one arrives at

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tilde{p} = \frac{8\tilde{t}}{3\tilde{v} -1} -\frac{3}{\tilde{v}^2}}

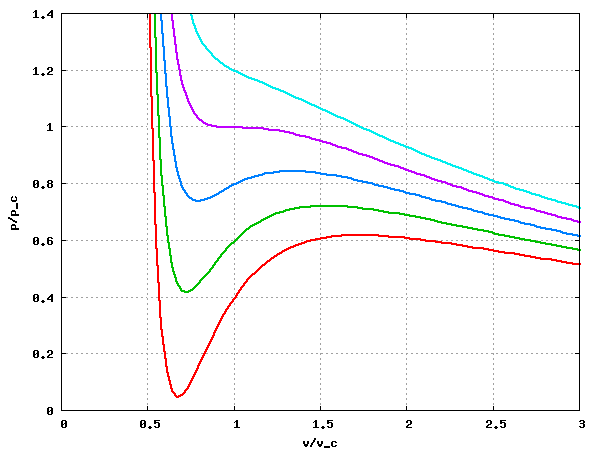
The following image is a plot of the isotherms Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T/T_c} = 0.85, 0.90, 0.95, 1.0 and 1.05 (from bottom to top) for the Van der Waals equation of state:

Plot of the isotherms T/T_c = 0.85, 0.90, 0.95, 1.0 and 1.05 for the Van der Waals equation of state

Interesting reading

• J. D. van der Waals "On the Continuity of the Gaseous and Liquid States", Dover Publications ISBN: 0486495930
• Johannes Diderik van der Waals "The Equation of State for Gases and Liquids", Nobel Lecture, December 12, 1910
• Luis Gonzalez MacDowell and Peter Virnau "El integrante lazo de Van der Waals", Anales de la Real Sociedad Española de Química 101 #1 pp. 19-30 (2005)