Capillary waves
Thermal capillary waves[edit]
Thermal capillary waves are oscillations of an interface which are thermal in origin. These take place at the molecular level, where only the contribution due to surface tension is relevant. Capillary wave theory is a classic account of how thermal fluctuations distort an interface (Ref. 1). It starts from some intrinsic surface that is distorted. In the Monge representation, the surface is given as . An increase in area of the surface causes a proportional increase of energy:
for small values of the derivatives (surfaces not too rough):
A Fourier analysis treatment begins by writing the intrinsic surface as an infinite sum of normal modes:
Since normal modes are orthogonal, the energy is easily expressible as a sum of terms . Each term of the sum is quadratic in the amplitude; hence equipartition holds, according to standard classical statistical mechanics, and the mean energy of each mode will be . Surprisingly, this result leads to a divergent surface (the width of the interface is bound to diverge with its area) (Ref 2). This divergence is nevertheless very mild; even for displacements on the order of meters, the deviation of the surface is comparable to the size of the molecules. Moreover, the introduction of an external field removes this divergence: the action of gravity is sufficient to keep the width fluctuation on the order of one molecular diameter for areas larger than about 1 mm2 (Ref. 2). The action of gravity is taken into account by integrating the potential energy density due to gravity, from a reference height to the position of the surface, :
(For simplicity, one neglects the density of the gas above, which is often acceptable; otherwise, instead of the density the difference in densities appears).
Recently, a procedure has been proposed to obtain a molecular intrinsic surface from simulation data (Ref. 3), the intrinsic sampling method. The density profiles obtained from this surface are, in general, quite different from the usual mean density profiles.
Gravity-capillary waves[edit]
These are ordinary waves excited in an interface, such as ripples on a water surface. Their dispersion relation reads, for waves on the interface between two fluids of infinite depth:
where is the angular frequency, the acceleration due to gravity, the surface tension, and the mass density of the two fluids () and the is wavenumber.
Derivation[edit]
This is a sketch of the derivation of the general dispersion relation, see Ref. 4 for a more detailed description. The problem is unfortunately a bit complex. As Richard Feynman put it (Ref. 6):
"...[water waves], which are easily seen by everyone and which are used as an example of waves in elementary courses... are the worst possible example... they have all the complications that waves can have"
Defining the problem[edit]
Three contributions to the energy are involved: the surface tension, gravity, and hydrodynamics. The parts due to surface tension (again the derivatives are taken to be small) and gravity are exactly as above. The new contribution involves the kinetic energy of the fluid:
where is the module of the velocity field . (Again, we are neglecting the flow of the gas above for simplicity.)
Wave solutions[edit]
Let us suppose the surface of the liquid is described by a traveling plane wave:
where and is a two dimensional wave number vector, being the horizontal position. We may take without loss of generality:
In this case it is easy to perform the integrations involved in the expressions for the energies. The integration over can taken over a period of oscillation , then multiplied by the number of oscillations in our very large (in principle, infinite) system: . The integration over trivially yields . Performing the integrations, keeping in mind that only the real part of complex numbers is to be taken as physical, one finds:
where is the area of the system.
To tackle the kinetic energy, suppose the fluid is incompressible and its flow is irrotational (often, sensible approximations) - the flow will then be potential: , and is a potential (scalar field) which must satisfy Laplace's equation . If we try try separation of variables with the potential:
with some function of time , and some function of vertical component (height) . Laplace's equation then requires on the later
This equation can be solved with the proper boundary conditions: first, must vanish well below the surface (in the "deep water" case, which is the one we consider, otherwise a more general relation holds, which is also well known in oceanography). Therefore
- ,
with some constant . The less trivial condition is the proper matching between and : the potential field must correspond to a velocity field that is adjusted to the movement of the surface:
- .
(Actually, this is the linearized version of a more general expression, see below.)
This implies that:
- , and
so that
- .
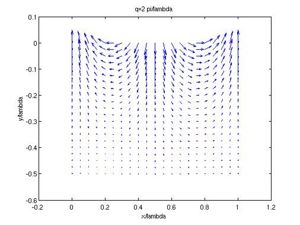
We may now find the velocity field, , which shows the well-known circles: the elements of fluid undergo circular motion in the plane, with the circles getting smaller at deeper levels. The displacement of a fluid element is given by , and is plotted in Figure 1.
For the kinetic energy, we need , which is:
with no dependence on or ; the other integration provides:
The problem is thus specified by just a potential energy involving the square of and a kinetic energy involving the square of its time derivative: a regular harmonic oscillator. In particular:
Identifying the oscillator's "spring constant" , and its "mass" , the oscillation frequency must be given by , which results in:
the same dispersion as above if is neglected.
Alternative derivation[edit]
In Reference 7 the dispersion relation is derived in a somewhat different manner. The same assumptions are made regarding the fluid (it is inviscid, irrotational, and incompressible), so Laplace's Equation is to be satisfied: , with . The boundary conditions, on the other hand, are sufficient to solve the problem.
One boundary condition is the requirement that the surface of the liquid, defined by follows the velocity field:
A simpler condition follows from linearization: , as in the previous derivation. There is an additional boundary condition at the bottom of the fluid, which we take here as when .
In the same fashion as above, we seek surface wave solutions, of the form . We may guess a solution of the form
This first condition implies . Together with Laplace's equation, this leads to a function
(see Ref 8 for a discussion on when Laplace's equation admits wave solutions.)
The other surface boundary condition is a Bernoulli equation, stating that the pressure just below the surface, , must equal the saturation pressure of coexistence, minus a contribution due to the surface:
The linearized condition is
The connection with the curvature of the surface can be introduced by Young's equation for the pressure drop across a curved interface, whose linearized form is:
where is the surface tension. The linearized condition is finally
This second condition, when applied to the surface wave above, establishes that .
For the two conditions to hold, must equal , which is precisely the same dispersion relation as the one above.
This derivation makes clear the assumptions introduced. In particular, the linearization will only hold for smooth waves, the ones for which the wave amplitude, is smaller than the wavelength. Mathematically, the limit is . For ocean waves, this happens when waves approach the shore and the amplitude grows (in this limit, a bottom boundary condition must be employed, and waves are not dispersive, see Ref 7.)
References[edit]
- F. P. Buff, R. A. Lovett, and F. H. Stillinger, Jr. "Interfacial density profile for fluids in the critical region" Physical Review Letters 15 pp. 621-623 (1965)
- J. S. Rowlinson and B. Widom "Molecular Theory of Capillarity". Dover 2002 (originally: Oxford University Press 1982) ISBN 0486425444
- E. Chacón and P. Tarazona "Intrinsic profiles beyond the capillary wave theory: A Monte Carlo study", Physical Review Letters 91 166103 (2003)
- Samuel A. Safran "Statistical thermodynamics of surfaces, interfaces, and membranes" Addison-Wesley 1994 ISBN 9780813340791
- P. Tarazona, R. Checa, and E. Chacón "Critical Analysis of the Density Functional Theory Prediction of Enhanced Capillary Waves", Physical Review Letters 99 196101 (2007)
- R.P. Feynman, R.B. Leighton, and M. Sands "The Feynman lectures on physics" Addison-Wesley 1963. Section 51-4. ISBN 0201021153
- W.K. Melville "Surface, gravity and capillary waves", in "Encyclopedia of Ocean Sciences", Eds: Steve A. Thorpe and Karl K. Turekian. Elsevier 2001, page 2916. ISBN 978-0-12-227430-5
- F Behroozi "Fluid viscosity and the attenuation of surface waves: a derivation based on conservation of energy", European Journal of Physics 25 115 (2004)


![{\displaystyle E_{\mathrm {st} }\approx {\frac {\sigma }{2}}\iint dx\,dy\ \left[\left({\frac {dh}{dx}}\right)^{2}+\left({\frac {dh}{dy}}\right)^{2}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/769a16c4785a579a9438c6c00dd884804dea4c04)

















![{\displaystyle \eta (t)=\exp[i\omega t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad7c036c5c4d8decaa7fbb211ff430363b37c9aa)
































![{\displaystyle E={\frac {A}{2}}\left[\left(\rho g+{\sigma }q^{2}\right){\frac {\eta ^{2}}{2}}+{\frac {\rho }{q}}{\frac {(\eta ')^{2}}{2}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8d51d8f3a41a4fc09ad4a2cb52bfe724562d03a8)















![{\displaystyle p_{-}=p-\rho \left[{\frac {\partial \phi }{\partial t}}+{\frac {1}{2}}v^{2}+gh\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4955b6d2d728b792740235e9e5b7bf8e0de2e25e)







