Van der Waals equation of state
The van der Waals equation of state, developed by Johannes Diderik van der Waals [1] [2], takes into account two features that are absent in the ideal gas equation of state; the parameter introduces somehow the repulsive behavior between pairs of molecules at short distances, it represents the minimum molar volume of the system, whereas measures the attractive interactions between the molecules. The van der Waals equation of state leads to a liquid-vapor equilibrium at low temperatures, with the corresponding critical point.
Equation of state
The van der Waals equation of state can be written as
where:
- is the pressure,
- is the volume,
- is the number of moles,
- is the absolute temperature,
- is the molar gas constant; , with being the Avogadro constant and being the Boltzmann constant.
- and are constants that introduce the effects of attraction and volume respectively and depend on the substance in question.
Critical point
At the critical point one has , and , leading to
along with a critical point compressibility factor of
which then leads to
Virial form
One can re-write the van der Waals equation given above as a virial equation of state as follows:
Using the well known series expansion one can write the first term of the right hand side as [3]:
Incorporating the second term of the right hand side in its due place leads to:
- .
From the above one can see that the second virial coefficient corresponds to
and the third virial coefficient is given by
Boyle temperature
The Boyle temperature of the van der Waals equation is given by
leading to
Dimensionless formulation
If one takes the following reduced quantities
one arrives at
The following image is a plot of the isotherms = 0.85, 0.90, 0.95, 1.0 and 1.05 (from bottom to top) for the van der Waals equation of state:
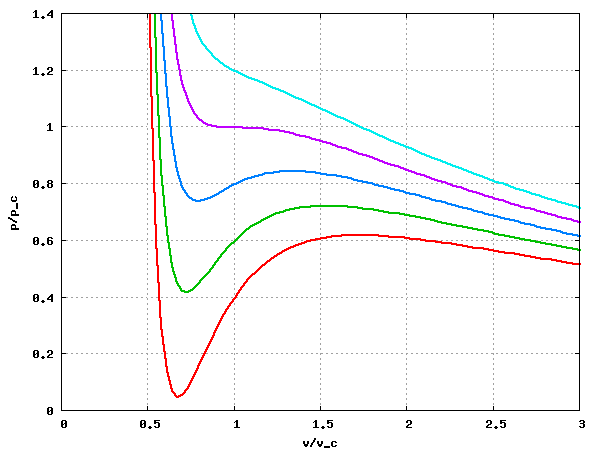
Critical exponents
The critical exponents of the Van der Waals equation of state place it in the mean field universality class.
See also
References
- ↑ J. D. van der Waals "Over de Continuiteit van den Gas- en Vloeistoftoestand", doctoral thesis, Leiden, A,W, Sijthoff (1873)
- ↑ English translation: J. D. van der Waals "On the Continuity of the Gaseous and Liquid States", Dover Publications ISBN: 0486495930
- ↑ This expansion is valid as long as , which is indeed the case for
Related reading
- Johannes Diderik van der Waals "The Equation of State for Gases and Liquids", Nobel Lecture, December 12, 1910
- Luis Gonzalez MacDowell and Peter Virnau "El integrante lazo de van der Waals", Anales de la Real Sociedad Española de Química 101 #1 pp. 19-30 (2005)































