TIP4P/Ice model of water: Difference between revisions
Jump to navigation
Jump to search
Carl McBride (talk | contribs) m (Started a section on the Liquid-vapour equilibria) |
m (→Parameters: Updated image) |
||
| Line 3: | Line 3: | ||
TIP4P/ice is a rigid planar model, having a similar geometry to the Bernal and Fowler ([[BF]]) model. | TIP4P/ice is a rigid planar model, having a similar geometry to the Bernal and Fowler ([[BF]]) model. | ||
==Parameters== | ==Parameters== | ||
[[Image: | [[Image:Four_site_water_model.png|center|400px]] | ||
| Line 15: | Line 15: | ||
*[[DL_POLY FIELD file for the TIP4P/ice model]] | *[[DL_POLY FIELD file for the TIP4P/ice model]] | ||
*[[GROMACS topology file for the TIP4P/ice model]] | *[[GROMACS topology file for the TIP4P/ice model]] | ||
==Liquid-vapour equilibria== | ==Liquid-vapour equilibria== | ||
*[http://dx.doi.org/10.1063/1.2215612 C. Vega, J. L. F. Abascal and I. Nezbeda "Vapor-liquid equilibria from the triple point up to the critical point for the new generation of TIP4P-like models: TIP4P/Ew, TIP4P/2005, and TIP4P/ice" Journal of Chemical Physics '''125''' 034503 (2006)] | *[http://dx.doi.org/10.1063/1.2215612 C. Vega, J. L. F. Abascal and I. Nezbeda "Vapor-liquid equilibria from the triple point up to the critical point for the new generation of TIP4P-like models: TIP4P/Ew, TIP4P/2005, and TIP4P/ice" Journal of Chemical Physics '''125''' 034503 (2006)] | ||
Revision as of 18:17, 8 June 2009
The TIP4P/ice model is a re-parameterisation of the original TIP4P potential for simulations of ice phases [1]. TIP4P/ice is a rigid planar model, having a similar geometry to the Bernal and Fowler (BF) model.
Parameters
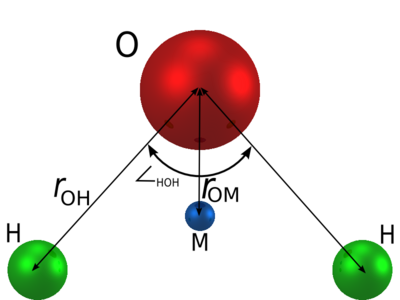
| (Å) | HOH , deg | (Å) | (K) | q(O) (e) | q(H) (e) | q(M) (e) | (Å) |
| 0.9572 | 104.52 | 3.1668 | 106.1 | 0 | 0.5897 | -2q(H) | 0.1577 |




