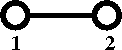Mayer f-function: Difference between revisions
Jump to navigation
Jump to search
Carl McBride (talk | contribs) |
Carl McBride (talk | contribs) No edit summary |
||
| Line 1: | Line 1: | ||
The '''Mayer ''f''-function''', or ''f-bond'' is defined as: | The '''Mayer ''f''-function''', or ''f-bond'' is defined as (Ref. 1 Chapter 13 Eq. 13.2): | ||
:<math>f_{12}=f({\mathbf r}_{12})= \exp\left(-\frac{\Phi_{12}(r)}{k_BT}\right) -1 </math> | :<math>f_{12}=f({\mathbf r}_{12})= \exp\left(-\frac{\Phi_{12}(r)}{k_BT}\right) -1 </math> | ||
Revision as of 14:50, 31 July 2007
The Mayer f-function, or f-bond is defined as (Ref. 1 Chapter 13 Eq. 13.2):
where
- is the Boltzmann constant.
- is the temperature.
- is the intermolecular pair potential.
Diagrammatically the Mayer f-function is written as
Hard sphere model
For the hard sphere model the Mayer f-function becomes:
where is the hard sphere diameter.
References
- Joseph Edward Mayer and Maria Goeppert Mayer "Statistical Mechanics" John Wiley and Sons (1940)
- Joseph E. Mayer "Contribution to Statistical Mechanics", Journal of Chemical Physics 10 pp. 629-643 (1942)