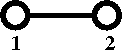Mayer f-function: Difference between revisions
Jump to navigation
Jump to search
Carl McBride (talk | contribs) No edit summary |
Carl McBride (talk | contribs) |
||
| Line 23: | Line 23: | ||
where <math>\sigma</math> is the hard sphere diameter. | where <math>\sigma</math> is the hard sphere diameter. | ||
==References== | ==References== | ||
# Joseph Edward Mayer and Maria Goeppert Mayer "Statistical Mechanics" John Wiley and Sons (1940) | |||
#[http://dx.doi.org/10.1063/1.1723631 Joseph E. Mayer "Contribution to Statistical Mechanics", Journal of Chemical Physics '''10''' pp. 629-643 (1942)] | #[http://dx.doi.org/10.1063/1.1723631 Joseph E. Mayer "Contribution to Statistical Mechanics", Journal of Chemical Physics '''10''' pp. 629-643 (1942)] | ||
[[Category: Statistical mechanics]] | [[Category: Statistical mechanics]] | ||
[[Category: Integral equations]] | [[Category: Integral equations]] | ||
Revision as of 14:49, 31 July 2007
The Mayer f-function, or f-bond is defined as:
where
- is the Boltzmann constant.
- is the temperature.
- is the intermolecular pair potential.
Diagrammatically the Mayer f-function is written as
Hard sphere model
For the hard sphere model the Mayer f-function becomes:
where is the hard sphere diameter.
References
- Joseph Edward Mayer and Maria Goeppert Mayer "Statistical Mechanics" John Wiley and Sons (1940)
- Joseph E. Mayer "Contribution to Statistical Mechanics", Journal of Chemical Physics 10 pp. 629-643 (1942)