Hertzian sphere model: Difference between revisions
Jump to navigation
Jump to search
Carl McBride (talk | contribs) (New page: The '''Hertzian sphere model''' is given by <ref>[http://dx.doi.org/10.1063/1.3186742 Josep C. Pàmies, Angelo Cacciuto, and Daan Frenkel "Phase diagram of Hertzian spheres", Journal of Ch...) |
Carl McBride (talk | contribs) m (Added a couple of recent publications) |
||
| (2 intermediate revisions by the same user not shown) | |||
| Line 9: | Line 9: | ||
</math> | </math> | ||
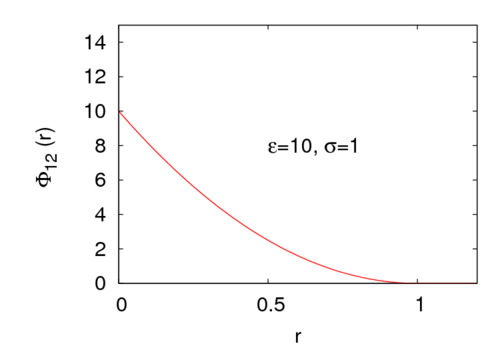
where <math> \Phi_{12}\left( r \right) </math> is the [[intermolecular pair potential]], <math>r := |\mathbf{r}_1 - \mathbf{r}_2|</math> is the distance between site 1 and site 2. <math>\sigma</math> represents a length scale and <math>\epsilon</math> an energy. In the limit <math>k_BT/\epsilon \rightarrow 0</math> this potential becomes the [[hard sphere model]]. | where <math> \Phi_{12}\left( r \right) </math> is the [[intermolecular pair potential]], <math>r := |\mathbf{r}_1 - \mathbf{r}_2|</math> is the distance between site 1 and site 2. <math>\sigma</math> represents a length scale and <math>\epsilon</math> an energy. In the limit <math>k_BT/\epsilon \rightarrow 0</math> this potential becomes the [[hard sphere model]]. For example, for <math>\epsilon=10</math> the potential looks like | ||
:[[Image:Hertzian_sphere.png|500px]] | |||
==See also== | |||
*[[Harmonic repulsion potential]] | |||
==References== | ==References== | ||
<references/> | <references/> | ||
;Related reading | |||
*[http://dx.doi.org/10.1063/1.3592563 Jian Yang and Kenneth S. Schweizer "Glassy dynamics and mechanical response in dense fluids of soft repulsive spheres. I. Activated relaxation, kinetic vitrification, and fragility", Journal of Chemical Physics '''134''' 204908 (2011)] | |||
*[http://dx.doi.org/10.1063/1.3592565 Jian Yang and Kenneth S. Schweizer "Glassy dynamics and mechanical response in dense fluids of soft repulsive spheres. II. Shear modulus, relaxation-elasticity connections, and rheology", Journal of Chemical Physics '''134''' 204909 (2011)] | |||
[[category: models]] | [[category: models]] | ||
Latest revision as of 11:46, 27 May 2011
The Hertzian sphere model is given by [1] (Eq. 1):
where is the intermolecular pair potential, is the distance between site 1 and site 2. represents a length scale and an energy. In the limit this potential becomes the hard sphere model. For example, for the potential looks like
See also[edit]
References[edit]
- Related reading
- Jian Yang and Kenneth S. Schweizer "Glassy dynamics and mechanical response in dense fluids of soft repulsive spheres. I. Activated relaxation, kinetic vitrification, and fragility", Journal of Chemical Physics 134 204908 (2011)
- Jian Yang and Kenneth S. Schweizer "Glassy dynamics and mechanical response in dense fluids of soft repulsive spheres. II. Shear modulus, relaxation-elasticity connections, and rheology", Journal of Chemical Physics 134 204909 (2011)