Fused hard sphere chains
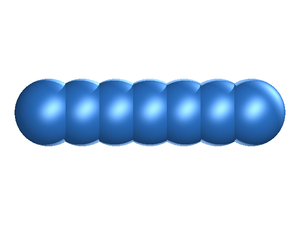
In the fused hard sphere chain model the molecule is built up form a string of overlapping hard sphere sites, each of diameter .
An effective number of monomers can be applied to the fused hard sphere chain model by using the relarion (Ref. [1] Eq. 2.18)
where is the number of monomer units in the model, and is the reduced bond length.
The volume of the fused hard sphere chain is given by (Ref. [2] Eq. 13)
where is the minimal bond angle, and the surface area is given by (Ref.[2] Eq. 12)
Equation of state[edit]
The Vörtler and Nezbeda equation of state is given by [3]
where
and
The Waziri and Hamad equation of state for fused hard sphere chain fluids is given by [4]
where
See also[edit]
References[edit]
- ↑ Yaoqi Zhou, Carol K. Hall and George Stell "Thermodynamic perturbation theory for fused hard-sphere and hard-disk chain fluids", Journal of Chemical Physics 103 pp. 2688-2695 (1995)
- ↑ 2.0 2.1 T. Boublík, C. Vega, and M. Diaz-Peña "Equation of state of chain molecules", Journal of Chemical Physics 93 pp. pp. 730-736 (1990)
- ↑ Horst L. Vörtler and I. Nezbeda "Volume-explicit equation of state and excess volume of mixing of fused hard sphere fluids", Berichte der Bunsen-Gesellschaft 94 pp. 559-563 (1990)
- ↑ Saidu M. Waziri and Esam Z. Hamad "Volume-Explicit Equation of State for Fused Hard Sphere Chain Fluids", Industrial & Engineering Chemistry Research 47 pp. 9658-9662 (2008)
- Related reading
- M. Whittle and A. J. Masters "Liquid crystal formation in a system of fused hard spheres", Molecular Physics 72 pp. 247-265 (1991)
- Carl McBride, Carlos Vega, and Luis G. MacDowell "Isotropic-nematic phase transition: Influence of intramolecular flexibility using a fused hard sphere model" Physical Review E 64 011703 (2001)
- Carl McBride and Carlos Vega "A Monte Carlo study of the influence of molecular flexibility on the phase diagram of a fused hard sphere model", Journal of Chemical Physics 117 pp. 10370-10379 (2002)
- Antoine Chamoux and Aurelien Perera "On the linear hard sphere chain fluids", Molecular Physics '93 pp. 649-661 (1998)

![{\displaystyle m_{\rm {effective}}={\frac {[1+(m-1)L^{*}]^{3}}{[1+(m-1)L^{*}(3-L^{*2})/2]^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/87c971dcd843e41062d341bfbcd501f4edea8001)





![{\displaystyle Z_{\mathrm {FHSC} }=1+(1+3\alpha )\eta _{0}(P^{*})+C_{\rm {FHSC}}[\eta _{0}(P^{*})]^{1.83}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/91afdc922fdfa04c21cdd02b43bebbdcfee850a4)
![{\displaystyle C_{\rm {FHSC}}=5.66\alpha (1-0.045[\alpha -1]^{1/2}\eta _{0})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4149ca3dad157caa5ae90ae3f5937fe4ef96457e)

![{\displaystyle Z_{\mathrm {FHSC} }=1+4m_{\mathrm {eff} }P^{*}+{\frac {3}{4}}m_{\mathrm {eff} }P^{*}\ln \left[{\frac {3+P^{*}}{3+25P^{*}}}\right]+{\frac {216(m_{\mathrm {eff} }-1)P^{*}}{(3+P^{*})(3+25P^{*})\{16+3\ln[(3+P^{*})/(3+25P^{*})]\}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/14883bcaf0a2995db20fbd4f59e80d64d62d9a07)
