Fused hard sphere chains

Example of the fused hard sphere chain model, shown here in a linear configuration.

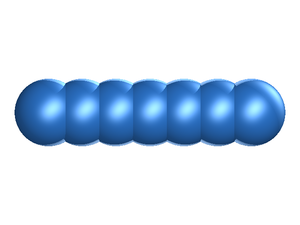
In the fused hard sphere chain model the molecule is built up form a string of overlapping hard sphere sites, each of diameter Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma} .

An effective number of monomers can be applied to the fused hard sphere chain model by using the relarion (Ref. 4 Eq. 2.18)

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_{\rm effective} = \frac{[1+(m-1)L^*]^3}{[1+(m-1)L^*(3-L^{*2})/2]^2}}

where m is the number of monomer units in the model, and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L^*=L/\sigma} is the reduced bond length.

The volume of the fused hard sphere chain is given by (Ref. 5 Eq. 13)

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_{\rm FHSC} =\frac{1}{6} \pi \sigma^3 \left( 1 + \frac{m-1}{2}L^* \left(3-L^{*2}\right) \right)}

and the surface area is given by (Ref. 5 Eq. 12)

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{\rm FHSC} = \pi \sigma^2 \left( 1+\left( m-1 \right) L^* \right)}

See also

• Rigid fully flexible fused hard sphere model

References

1. M. Whittle and A. J. Masters "Liquid crystal formation in a system of fused hard spheres", Molecular Physics 72 pp. 247-265 (1991)
2. Carl McBride, Carlos Vega, and Luis G. MacDowell "Isotropic-nematic phase transition: Influence of intramolecular flexibility using a fused hard sphere model" Physical Review E 64 011703 (2001)
3. Carl McBride and Carlos Vega "A Monte Carlo study of the influence of molecular flexibility on the phase diagram of a fused hard sphere model", Journal of Chemical Physics 117 pp. 10370-10379 (2002)
4. Yaoqi Zhou, Carol K. Hall and George Stell "Thermodynamic perturbation theory for fused hard-sphere and hard-disk chain fluids", Journal of Chemical Physics 103 pp. 2688-2695 (1995)
5. T. Boublík, C. Vega, and M. Diaz-Peña "Equation of state of chain molecules", Journal of Chemical Physics 93 pp. pp. 730-736 (1990)