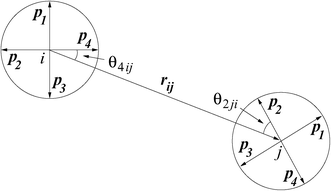
Modulated patchy Lennard-Jones model
The modulated patchy Lennard-Jones model is given by [1] (Eqs. 4.3 and 4.4)
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi_{\mathrm {patchy}}({\mathbf r}_{ij},{\mathbf \Omega}_i,{\mathbf \Omega}_j) = \left\{ \begin{array}{lll} \Phi_{\mathrm {LJ}}(r_{ij}) & ; & r_{ij} < \sigma_{\mathrm {LJ}} \\ \Phi_{\mathrm{LJ}}(r_{ij}) \exp \left(-\frac{\theta_{k_{min},ij}^2}{2\sigma^2 } \right) \exp \left(-\frac{\theta_{l_{min},ji}^2}{2\sigma^2 } \right) & ; & r_{ij} \ge \sigma_{\mathrm{LJ}} \end{array} \right. }
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi_{\mathrm {LJ}}(r_{ij})} is the Lennard-Jones potential and