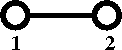Mayer f-function

The Mayer f-function, or f-bond is defined as (Ref. 1 Chapter 13 Eq. 13.2):

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f_{12}=f({\mathbf r}_{12})= \exp\left(-\frac{\Phi_{12}(r)}{k_BT}\right) -1 }

where

• Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_B} is the Boltzmann constant.
• Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T} is the temperature.
• $\Phi _{12}(r)$ is the intermolecular pair potential.

In other words, the Mayer function is the Boltzmann factor of the interaction potential, minus one.

Diagrammatically the Mayer f-function is written as

Hard sphere model

For the hard sphere model the Mayer f-function becomes:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f_{12}= \left\{ \begin{array}{lll} -1 & ; & r_{12} \leq \sigma ~~({\rm overlap})\\ 0 & ; & r_{12} > \sigma ~~({\rm no~overlap})\end{array} \right. }

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma} is the hard sphere diameter.

References

1. Joseph Edward Mayer and Maria Goeppert Mayer "Statistical Mechanics" John Wiley and Sons (1940)
2. Joseph E. Mayer "Contribution to Statistical Mechanics", Journal of Chemical Physics 10 pp. 629-643 (1942)