Smectic phases: Difference between revisions
Carl McBride (talk | contribs) No edit summary |
Carl McBride (talk | contribs) |
||
| Line 4: | Line 4: | ||
==Smectic A phase== | ==Smectic A phase== | ||
In the smectic-A phase each layer is a 2-dimensional liquid, having the symmetry <math>D_\infty</math> in the Schoenflies notation. | In the smectic-A phase each layer is a 2-dimensional liquid, having the symmetry <math>D_\infty</math> in the Schoenflies notation. | ||
*[http://dx.doi.org/10.1103/PhysRevA.4.1238 W. L. McMillan "Simple Molecular Model for the Smectic A Phase of Liquid Crystals", Physical Review A '''4''' pp. 1238 - 1246 (1971)] | |||
==Smectic B phase== | ==Smectic B phase== | ||
==Smectic C phase== | ==Smectic C phase== | ||
Revision as of 17:54, 29 August 2007
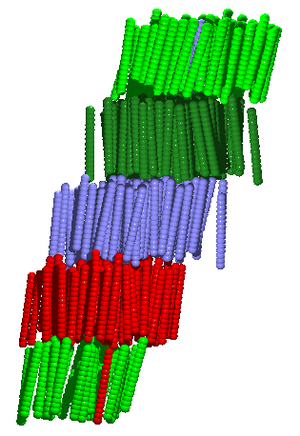
The work smectic comes from the Greek for soap (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma \mu \acute{\eta} \gamma \mu \alpha} ). All of the smectic phases are layered, belonging to the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G_1^3} symmetry group.
Smectic A phase
In the smectic-A phase each layer is a 2-dimensional liquid, having the symmetry Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D_\infty} in the Schoenflies notation.
Smectic B phase
Smectic C phase
The smectic-C phase has the monoclinic symmetry Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_{\rm 2h}} .