Ramp model

The ramp model, proposed by Jagla and sometimes known as the Jagla model, is described by:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi_{12}(r) = \left\{ \begin{array}{ll} \infty & {\rm if} \; r < \sigma \\ W_r - (W_r-W_a) \frac{r-\sigma}{d_a-\sigma} & {\rm if} \; \sigma \leq r \leq d_a \\ W_a - W_a \frac{r-d_a}{d_c-d_a} & {\rm if} \; d_a < r \leq d_c \\ 0 & {\rm if} \; r > d_c \end{array} \right. }

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi_{12}(r)} is the intermolecular pair potential, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r := |\mathbf{r}_1 - \mathbf{r}_2|} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle W_r > 0} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle W_a < 0} .

Graphically, one has:

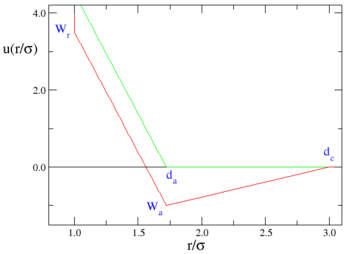
where the red line represents an attractive implementation of the model, and the green line a repulsive implementation.

Critical points

For the particular case $W_{r}^{*}=3.5;W_{a}^{*}=-1.0,d_{a}^{*}=1.72,d_{c}^{*}=3.0$, the liquid-vapour critical point is located at :

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_c^* = 1.487 \pm 0.003}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho_c \sigma^3 = 0.103 \pm 0.001}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p_c^* \simeq 0.042}

and the liquid-liquid critical point:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_c^* \simeq 0.378 \pm 0.003}

$\rho _{c}\sigma ^{3}\simeq 0.380\pm 0.002$

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p_c^*/T_c^* \simeq 0.49 \pm 0.01}

Repulsive Ramp Model

In the repulsive ramp case, where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle W_a = 0 } , neither liquid-vapor nor liquid-liquid stable equilibria occur . However, for this model a low density crystalline phase has been found. This solid phase presents re-entrant melting, i.e. this solid melts into the fluid phase as the pressure is increased.

Lattice gas version

Recently, similar behaviour has been found in a three-dimensional Repulsive Ramp Lattice Gas model The system is defined on a simple cubic lattice. The interaction is that of a lattice hard sphere model with exclusion of nearest neighbours of occupied positions plus a repulsive interaction with next-to-nearest neighbours. The total potential energy of the system is then given by:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U = \epsilon \sum_{[ij]} S_i S_j }

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon > 0 }  ; Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [ij] } refers to all the pairs of sites that are second neighbors, and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_k } indicates the occupation of site Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k } (0 indicates an empty site, 1 indicates an occupied site).

See also

• Triangular lattice ramp model
• Polyamorphism: Ramp model

References

Related literature

• Limei Xu, Sergey V. Buldyrev, C. Austen Angell, and H. Eugene Stanley "Thermodynamics and dynamics of the two-scale spherically symmetric Jagla ramp model of anomalous liquids", Physical Review E 74 031108 (2006)
• Limei Xu, Sergey V. Buldyrev, Nicolas Giovambattista, C. Austen Angell, and H. Eugene Stanley "A monatomic system with a liquid-liquid critical point and two distinct glassy states", Journal of Chemical Physics 130 054505 (2009)
• Limei Xu, Sergey V. Buldyrev, Nicolas Giovambattista, and H. Eugene Stanley "Liquid-Liquid Phase Transition and Glass Transition in a Monoatomic Model", International Journal of Molecular Sciences 11 pp. 5184-5200 (2010)