Uhlenbeck-Ford model
The Uhlenbeck-Ford model (UFM), originally named Gaussian gas [1], was proposed by G. Uhlenbeck and G. Ford [2] for the theoretical study of imperfect gases. This model is characterized by an ultrasoft, purely repulsive pairwise interaction potential that diverges logarithmically at the origin and features an energy scale that coincides with the thermal energy unit where is the Boltzmann constant and the absolute temperature. The particular functional form of the potential permits, in principle, that the virial coefficients and, therefore, the equation of state and excess free energies for the fluid phase be evaluated analytically. A recent study [3] showed that this model can be used as a reference system for fluid-phase free-energy calculations.
Functional form[edit]
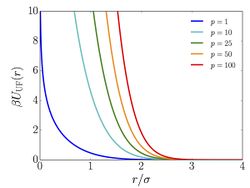
The pairwise interaction potential associated with the Uhlenbeck-Ford model is given by
- ,
where
- is a scaling factor.
- is the well depth (energy).
- is the inter particle distance.
- is a length-scale parameter.
Note that increasing the value of gives rise to a stronger repulsion.
Equation of state[edit]
The equation of state for the UFM fluid using virial expansion has recently been studied by Paula Leite, Freitas, Azevedo and de Koning [3] and is given by
- ,
where
- is the system pressure.
- is a constant.
- is an adimensional variable.
- are the reduced virial coefficients.
Note that, due to the functional form of the potential, the equation of state for the UFM fluid can be specified in terms of a function of a single adimensional variable , regardless of the length-scale and absolute temperature , i.é., the virial coefficients are independent of the absolute temperature.
Excess Helmholtz free-energy[edit]
The excess Helmholtz free-energy expression for the UFM, which can be obtained integrating the equation of state with respect to volume [3], is given by
- ,
where
- is the excess Helmholtz free energy.
- is the number of particles.
Virial coefficients[edit]
As the virial coefficients for the UFM can be calculated analytically, in principle, Paula Leite, Freitas, Azevedo and de Koning [3] recalculated the first eight coefficients previously known to and obtained values for four new coefficients to for . Some coefficients for and are also shown in the table below.
Table 1: Numerical representation of the exact virial coefficients for the UFM.
p=1 p=2 p=10 1 1.646 446 609 40 4.014 383 975 40 0.256 600 119 639 833 673 11 0.943 195 827 15 8.031 625 170 36 -0.125 459 957 055 044 678 34 -0.334 985 180 88 5.791 113 868 79 0.013 325 655 173 205 441 00 -0.303 688 574 00 -7.658 371 037 27 0.038 460 935 830 869 671 55 0.395 857 781 68 -0.033 083 442 903 149 717 39 0.053 655 130 98 0.004 182 418 769 682 387 35 -0.408 481 406 00 0.015 197 607 195 500 874 66 -0.013 849 654 134 575 142 93 0.001 334 757 917 110 966 11 0.007 604 327 248 812 125 87 -0.006 726 441 408 781 588 25
Numerical representations[edit]
Due to the number of integrals needed to compute the virial coefficients, a numerical representation using molecular dynamics data is usually adopted. In this sense, extensive molecular dynamics simulations have been performed and using a piece-wise fitting procedure, called cubic splines, numerical expressions for the UFM's equation of state were constructed. Moreover, this representation also leads to an excellent description for the excess Helmholtz free energy .
All spline representations of equations of state and excess Helmholtz free energies are available by means of the python script ufGenerator.py supplied in the supplementary material of Paula Leite et al. paper [3].
Phase diagram[edit]
The phase diagram of the UFM in the has been constructed by Paula Leite, Santos-Flórez and de Koning [4]. Beyond the fluid phase, body-centered-cubic (bcc) and face-centered-cubic (fcc) are the only thermodynamically stable crystalline phases. These three phases meet each other at a triple point. Furthermore, they reported the existence of two reentrant transition sequences as a function of the number density, one featuring a fluid-bcc-fluid succession and another displaying a bcc-fcc-bcc sequence near the triple point.
Reference system[edit]
The UFM can be used as a reference system for fluid-phase free-energy calculations. Examples of these kind of calculations using thermodynamic integration techniques for different natures of fluid description (Lennard-Jones, Silicon-SW, CuZr-EAM-metallic glass, rigid and flexible water models) can be found in Paula Leite et al. paper [3]. Recently, water-like models using the UF model as an interacting potential were reported and added on LAMMPS source-code. The respective publication [5] and a complete guide [6] are available on reference section. The typical values for are .
References[edit]
- ↑ D. McQuarrie, Statistical Mechanics (University Science Books, 2000).
- ↑ G. Uhlenbeck and G. Ford, in Studies in Statistical Mechanics— The Theory of Linear Graphs with Application to the Theory of the Virial Development of the Properties of Gases, edited by G. E. Uhlenbeck and J. de Boer (North-Holland, Amsterdam, 1962), Vol. 2.
- ↑ 3.0 3.1 3.2 3.3 3.4 3.5 R. Paula Leite, R. Freitas, R. Azevedo and M. de Koning "The Uhlenbeck-Ford model: Exact virial coefficients and application as a reference system in fluid-phase free-energy calculations", Journal of Chemical Physics 145, 194101 (2016).
- ↑ 4.0 4.1 R. Paula Leite, P. A. Santos-Flórez and M. de Koning "Uhlenbeck-Ford model: Phase diagram and corresponding-states analysis", Physical Review E 96, 032115 (2017).
- ↑ R. Paula Leite, and M. de Koning "Nonequilibrium free-energy calculations of fluids using LAMMPS", Computational Material Science 159, 316-326 (2019).
- ↑ [1]






































