SALR potential
Jump to navigation
Jump to search
The SALR ( short-range attractive - long-range repulsive) potential. This potential has a variety of functional forms.
HCDY[edit]
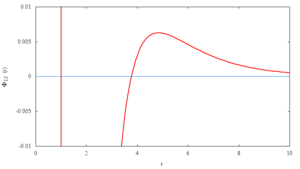
The SALR potential is often expressed as a hard core of diameter , along with combination of two Yukawa potentials:
where is the intermolecular pair potential, is the distance between site 1 and site 2.
The control is the energy of the repulsive and attractive parts, whilst the
controls the interaction range.
This potential also goes by the names of the hard-sphere plus two Yukawa (H2Y) or hard-core double-Yukawa (HCDY) potential [2][3][4] [5].
LJ+Y[edit]
Another SALR model consists of a generalised Lennard-Jones model in conjunction with a long-range repulsive Yukawa term [6] [7] [8] [9] [10]
References[edit]
- ↑ Martin B. Sweatman, Rui Fartaria, and Leo Lue "Cluster formation in fluids with competing short-range and long-range interactions", nal of Chemical Physics 140 124508 (2014)
- ↑ Yang-Zheng Lin, Yi-Gui Li, Jiu-Fang Lu and Wei Wu "Monte Carlo simulation for the hard-core two-Yukawa fluids and test of the two-Yukawa equation of state", Journal of Chemical Physics 117 10165 (2002)
- ↑ Lloyd L. Lee, Michael C. Hara, Steven J. Simon, Franklin S. Ramos, Andrew J. Winkle, and Jean-Marc Bomont "Crystallization limits of the two-term Yukawa potentials based on the entropy criterion", Journal of Chemical Physics 132 074505 (2010)
- ↑ J. Montes, M. Robles and M. López de Haro "Equation of state and critical point behavior of hard-core double-Yukawa fluids", Journal of Chemical Physics 144 084503 (2016)
- ↑ Andrew J. Archer and Nigel B. Wilding "Phase behavior of a fluid with competing attractive and repulsive interactions", Physical Review E 76 031501 (2007)
- ↑ Francesco Sciortino, Stefano Mossa, Emanuela Zaccarelli, and Piero Tartaglia "Equilibrium Cluster Phases and Low-Density Arrested Disordered States: The Role of Short-Range Attraction and Long-Range Repulsion", Physical Review Letters 93 055701 (2004)
- ↑ Ethayaraja Mani, Wolfgang Lechner, Willem K. Kegel and Peter G. Bolhuis "Equilibrium and non-equilibrium cluster phases in colloids with competing interactions", 10 pp. 4479-4486 (2014)
- ↑ Štěpán Růžička and Michael P. Allen "Monodisperse Clusters in Charged Attractive Colloids: Linear Renormalization of Repulsion", Journal of Chemical Theory and Computation 11 pp. 3811-3817 (2015)
- ↑ Andrew P. Santos Jakub Pȩkalski and Athanassios Z. Panagiotopoulos "Thermodynamic signatures and cluster properties of self-assembly in systems with competing interactions", Soft Matter 13 pp. 8055-8063 (2017)
- ↑ Jakub Pȩkalski, Andrew P. Santos, Athanassios Z. Panagiotopoulos "From Compact to Open Clusters in Systems with Competing Interactions", arXiv 1703.01213 (2017)
- Related reading





![{\displaystyle \Phi _{12}\left(r\right)=\left\{{\begin{array}{lll}\infty &;&r<\sigma \\\epsilon _{r}\left({\frac {\sigma }{r}}\right)\exp \left[-\kappa _{r}\left({\frac {r}{\sigma }}-1\right)\right]-\epsilon _{a}\left({\frac {\sigma }{r}}\right)\exp \left[-\kappa _{a}\left({\frac {r}{\sigma }}-1\right)\right]&;&r\geq \sigma \end{array}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/88d11cb9937adbdea30b82a5405ca24e51a28208)




![{\displaystyle \Phi _{12}(r)=4\epsilon \left[\left({\frac {\sigma }{r}}\right)^{2a}-\left({\frac {\sigma }{r}}\right)^{a}\right]+A{\frac {e^{-r/\xi }}{r/\xi }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/65ea2489c3e881c51287dbfc13da68d6223b5710)