Lattice simulations (Polymers)
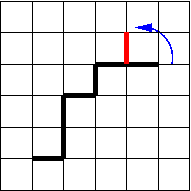
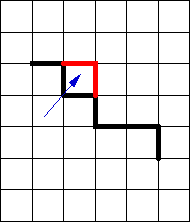
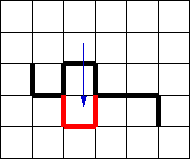
Polymers have many interesting mesoscopic properties that can adequately represented through coarse-grained models. Lattice models are particularly useful since they employ integer coordinates that can be quickly processed. Another advantage is the possibility of checking the occupancy of the discrete number of sites and store it in an array. Therefore, overlapping between beads can be easily avoided. Earlier simulations were performed with the simple cubic or tetrahedral lattices, employing different algorithms. Tetrahedral lattice models are mainly used because of their closer similarity of their bond angles with those of the aliphatic chains. Algorithms useful for lattice models may have special difficulties to comply with the ergodicity and microscopic reversibility conditions. Elementary bead jumps are commonly used to try to mimic dynamics [1]. Combinations of end rotations (figure 1), bend (or "kink") (figure 2) and crankshaft (figure 3) moves has been shown to be nearly ergodic and reproduce adequately the Rouse dynamics of single chain systems in a cubic lattice [2]. More efficient pivot moves have been devised to explore the equilibrium properties of very long single chains [3]. Although the lattice simulations can effectively represent melts, most algorithms employ a certain amount of voids to allow specific local motions. An exception is the cooperative motion algorithm that considers totally occupied systems [4]. Also, specific algorithms to perform isothermal-isobaric ensemble (NpT) simulations have been designed [5]. The bond fluctuation model has been proposed to combine the advantages of lattice and off-lattice models.
See also[edit]
References[edit]
- ↑ P. H. Verdier and W. H. Stockmayer "Monte Carlo Calculations on the Dynamics of Polymers in Dilute Solution", Journal of Chemical Physics 36 pp. 227-235 (1962)
- ↑ H. J. Hilhorst and J. M. Deutch "Analysis of Monte Carlo results on the kinetics of lattice polymer chains with excluded volume", Journal of Chemical Physics 63 pp. 5153-5161 (1975)
- ↑ Neal Madras and Alan D. Sokal "The pivot algorithm: A highly efficient Monte Carlo method for the self-avoiding walk", Journal of Statistical Physics 50 pp. 109-186 (1988)
- ↑ T. Pakula and S. Geyler "Cooperative relaxations in condensed macromolecular systems. 1. A model for computer simulation", Macromolecules 20 pp. 679-682 (1987)
- ↑ A. D. Mackie, A. Z. Panagiotopoulos, S. K. Kumar "Monte Carlo simulations of phase equilibria for a lattice homopolymer model", Journal of Chemical Physics 102 pp. 1014-1023 (1995)