Ramp model
The ramp model, proposed by Jagla [1] and sometimes known as the Jagla model, is described by:
where is the intermolecular pair potential, , and .
Graphically, one has:
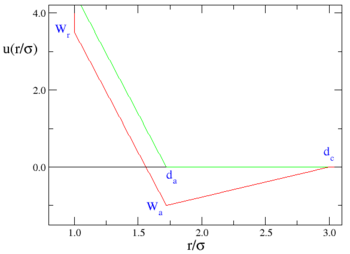
where the red line represents an attractive implementation of the model, and the green line a repulsive implementation.
Critical points[edit]
For the particular case , the liquid-vapour critical point is located at [2]:
and the liquid-liquid critical point:
While this liquid-liquid critical point was long held to be in the stable region of the phase diagram, a high density double-network structure was found to be thermodynamically more stable than the high-density liquid under any conditions.[3]:
Repulsive Ramp Model[edit]
In the repulsive ramp case, where , neither liquid-vapor nor liquid-liquid stable equilibria occur [2]. However, for this model a low density crystalline phase has been found. This solid phase presents re-entrant melting, i.e. this solid melts into the fluid phase as the pressure is increased.
Lattice gas version[edit]
Recently, similar behaviour has been found in a three-dimensional Repulsive Ramp Lattice Gas model [4] The system is defined on a simple cubic lattice. The interaction is that of a lattice hard sphere model with exclusion of nearest neighbours of occupied positions plus a repulsive interaction with next-to-nearest neighbours. The total potential energy of the system is then given by:
where ; refers to all the pairs of sites that are second neighbors, and indicates the occupation of site (0 indicates an empty site, 1 indicates an occupied site).
See also[edit]
References[edit]
- ↑ E. A. Jagla "Core-softened potentials and the anomalous properties of water", Journal of Chemical Physics' 111 pp. 8980-8986 (1999)
- ↑ 2.0 2.1 E. Lomba, N. G. Almarza, C. Martin, C. McBride "Phase behaviour of attractive and repulsive ramp fluids: integral equation and computer simulation studies", Journal of Chemical Physics 126 244510 (2007)
- ↑ A. P. Bartók, G. Hantal, L. B. Pártay "Insight into Liquid Polymorphism from the Complex Phase Behavior of a Simple Model", Physical Review Letters 127 015701 (2021)
- ↑ Johan Skule Hoye, Enrique Lomba, and Noe Garcia Almarza, "One- and three-dimensional lattice models with two repulsive ranges: simple systems with complex phase behaviour", Molecular Physics 107, 321-330 (2009)
Related literature
- Limei Xu, Sergey V. Buldyrev, C. Austen Angell, and H. Eugene Stanley "Thermodynamics and dynamics of the two-scale spherically symmetric Jagla ramp model of anomalous liquids", Physical Review E 74 031108 (2006)
- Limei Xu, Sergey V. Buldyrev, Nicolas Giovambattista, C. Austen Angell, and H. Eugene Stanley "A monatomic system with a liquid-liquid critical point and two distinct glassy states", Journal of Chemical Physics 130 054505 (2009)
- Limei Xu, Sergey V. Buldyrev, Nicolas Giovambattista, and H. Eugene Stanley "Liquid-Liquid Phase Transition and Glass Transition in a Monoatomic Model", International Journal of Molecular Sciences 11 pp. 5184-5200 (2010)
- Limei Xu, Nicolas Giovambattista, Sergey V. Buldyrev, Pablo G. Debenedetti, and H. Eugene Stanley "Waterlike glass polyamorphism in a monoatomic isotropic Jagla model", Journal of Chemical Physics 134 064507 (2011)
- Jiayuan Luo, Limei Xu, C. Austen Angell, H. Eugene Stanley and Sergey V. Buldyrev "Physics of the Jagla model as the liquid-liquid coexistence line slope varies", Journal of Chemical Physics 142 224501 (2015)













![{\displaystyle U=\epsilon \sum _{[ij]}S_{i}S_{j}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/47128ac7d19cf407aa50871277c85fc5139db8d1)

![{\displaystyle [ij]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4d30520e09683aad1e38713ce1a8182cde93c0ce)

