Hard superball model

The shape of superballs interpolates between octahedra (q = 0.5) and cubes (q = ∞) via spheres (q = 1).

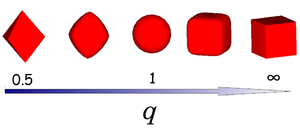
A superball is defined by the inequality

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left|\frac{x}{a}\right|^{2q} + \left|\frac{y}{a}\right|^{2q} +\left|\frac{z}{a}\right|^{2q} \le 1}

where x, y and z are scaled Cartesian coordinates with q the deformation parameter and radius a. The shape of the superball interpolates smoothly between two Platonic solids, namely the octahedron (q = 0.5) and the cube (q = ∞) via the sphere (q = 1) as shown in the left figure.