Patchy particles: Difference between revisions
Jump to navigation
Jump to search
m (Removed stub template) |
|||
| Line 1: | Line 1: | ||
The general model for a '''patchy particle''' is given by | The general model for a '''patchy particle''' is given by | ||
<ref>[http://dx.doi.org/10.1039/b614955c Jonathan P. K. Doye, Ard A. Louis, I-Chun Lin, Lucy R. Allen, Eva G. Noya, Alex W. Wilber, Hoong Chwan Kok and Rosie Lyus "Controlling crystallization and its absence: proteins, colloids and patchy models", Physical Chemistry Chemical Physics '''9''' pp. 2197-2205 (2007)]</ref> | <ref>[http://dx.doi.org/10.1039/b614955c Jonathan P. K. Doye, Ard A. Louis, I-Chun Lin, Lucy R. Allen, Eva G. Noya, Alex W. Wilber, Hoong Chwan Kok and Rosie Lyus "Controlling crystallization and its absence: proteins, colloids and patchy models", Physical Chemistry Chemical Physics '''9''' pp. 2197-2205 (2007)]</ref> | ||
Revision as of 16:26, 30 November 2009
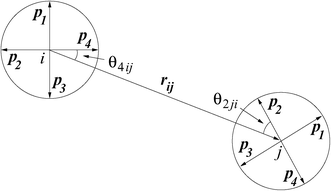
The general model for a patchy particle is given by [1]
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_{\mathrm {patchy}}({\mathbf r}_{ij},{\mathbf \Omega}_i,{\mathbf \Omega}_j) = \left\{ \begin{array}{lll} u_{\mathrm {LJ}}(r_{ij}) & ; & r_{ij} < \sigma_{\mathrm {LJ}} \\ u_{\mathrm{LJ}}(r_{ij}) \exp \left(-\frac{\theta_{k_{min},ij}^2}{2\sigma^2 } \right) \exp \left(-\frac{\theta_{l_{min},ji}^2}{2\sigma^2 } \right) & ; & r_{ij} \ge \sigma_{\mathrm{LJ}} \end{array} \right. }
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_{\mathrm {LJ}}(r_{ij})} is the Lennard-Jones potential and
See also
- Phase diagram of anisotropic particles with octahedral symmetry
- Phase diagram of anisotropic particles with tetrahedral symmetry