Lennard-Jones model

Lennard-Jones potential

The Lennard-Jones potential, developed by Sir John Edward Lennard-Jones, is given by

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi(r) = 4 \epsilon \left[ \left(\frac{\sigma}{r} \right)^{12}- \left( \frac{\sigma}{r}\right)^6 \right] }

where:

• Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi(r) } is the intermolecular pair potential between two particles at a distance r;

• $\sigma$ : diameter (length);

• Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon }  : well depth (energy)

Reduced units:

• Density, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho^* \equiv \rho \sigma^3 } , where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho = N/V } (number of particles Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N } divided by the volume $V$.)

• Temperature; Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T^* \equiv k_B T/\epsilon } , where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T } is the absolute temperature and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_B } is the Boltzmann constant

Argon

The Lennard-Jones parameters for argon are Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon/k_B \approx} 119.8 K and $\sigma \approx$ 0.3405 nm. (Ref. ?)

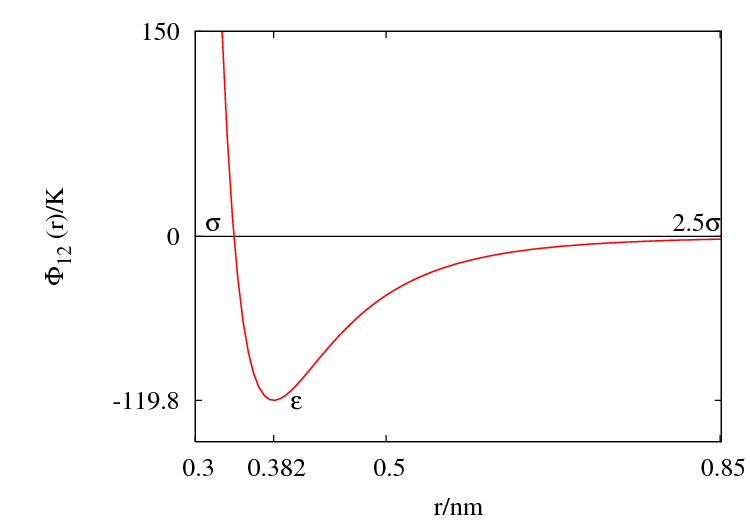
This figure was produced using gnuplot with the command:

plot (4*120*((0.34/x)**12-(0.34/x)**6))

Features

Special points:

• Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi(\sigma) = 0 }

• Minimum value of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi(r) } at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r = r_{min} } ;

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{r_{min}}{\sigma} = 2^{1/6} \simeq 1.12246 ... }

Related potential models

It is relatively common the use of potential functions given by:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi (r) = c_{m,n} \epsilon \left[ \left( \frac{ \sigma }{r } \right)^m - \left( \frac{\sigma}{r} \right)^n \right]. }

with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m } and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n } being positive integer numbers and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m > n } , and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c_{m,n} } is chosen to get the minimum value of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi(r) } being Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi_{min} = - \epsilon }

These forms are usually referred to as m-n Lennard-Jones Potential.

The 9-3 Lennard-Jones interaction potential is often use to model the interaction between the atoms/molecules of a fluid and a continuous solid wall. In (9-3 Lennard-Jones potential) a justification of this use is presented.

Other dimensions

• 1-dimensional case: Lennard-Jones rods.
• 2-dimensional case: Lennard-Jones disks.

References

1. J. E. Lennard-Jones, "Cohesion", Proceedings of the Physical Society, 43 pp. 461-482 (1931)