Radial distribution function: Difference between revisions
Carl McBride (talk | contribs) m (Updated a reference) |
|||
| Line 43: | Line 43: | ||
*[http://dx.doi.org/10.1143/JPSJ.12.326 Kazuo Hiroike "Radial Distribution Function of Fluids I", Journal of the Physical Society of Japan '''12''' pp. 326-334 (1957)] | *[http://dx.doi.org/10.1143/JPSJ.12.326 Kazuo Hiroike "Radial Distribution Function of Fluids I", Journal of the Physical Society of Japan '''12''' pp. 326-334 (1957)] | ||
*[http://dx.doi.org/10.1143/JPSJ.12.864 Kazuo Hiroike "Radial Distribution Function of Fluids II", Journal of the Physical Society of Japan '''12''' pp. pp. 864-873 (1957)] | *[http://dx.doi.org/10.1143/JPSJ.12.864 Kazuo Hiroike "Radial Distribution Function of Fluids II", Journal of the Physical Society of Japan '''12''' pp. pp. 864-873 (1957)] | ||
*[http://dx.doi.org/10.1080/00268970701678907 J. G. Malherbe and Krauth "Selective-pivot sampling of radial distribution functions in asymmetric liquid mixtures", Molecular Physics ( | *[http://dx.doi.org/10.1080/00268970701678907 J. G. Malherbe and W. Krauth "Selective-pivot sampling of radial distribution functions in asymmetric liquid mixtures", Molecular Physics '''105''' pp. 2393-2398 (2007)] | ||
*[http://doi.org/10.1063/1.4973804 Sergey V. Sukhomlinov, Martin H. Müser "Determination of accurate, mean bond lengths from radial distribution functions", Journal of Chemical Physics '''146''' 024506 (2017)] | *[http://doi.org/10.1063/1.4973804 Sergey V. Sukhomlinov, Martin H. Müser "Determination of accurate, mean bond lengths from radial distribution functions", Journal of Chemical Physics '''146''' 024506 (2017)] | ||
[[category: statistical mechanics]] | [[category: statistical mechanics]] | ||
Latest revision as of 10:18, 8 October 2019
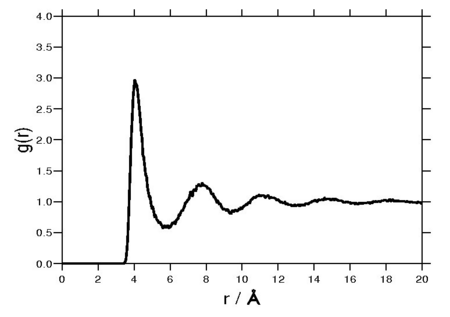
The radial distribution function is a special case of the pair distribution function for an isotropic system. A Fourier transform of the radial distribution function results in the structure factor, which is experimentally measurable. The following plot is of a typical radial distribution function for the monatomic Lennard-Jones liquid.
Density Expansion of the radial distribution function[edit]
The radial distribution function of a compressed gas may be expanded in powers of the density [1]
where is the number of molecules per unit volume and is the intermolecular pair potential. The function is normalized to the value 1 for large distances. As is known, , , ... can be expressed by cluster integrals in which the position of of two particles is kept fixed. In classical mechanics, and on the assumption of additivity of intermolecular forces, one has
where is the distance , where is the Mayer f-function
and
See also[edit]
References[edit]
- Related reading
- John G. Kirkwood and Elizabeth Monroe Boggs "The Radial Distribution Function in Liquids", Journal of Chemical Physics 10 pp. 394-402 (1942)
- J. L. Lebowitz and J. K. Percus "Asymptotic Behavior of the Radial Distribution Function", Journal of Mathematical Physics 4 pp. 248-254 (1963)
- B. Widom "On the Radial Distribution Function in Fluids", Journal of Chemical Physics 41 pp. 74-77 (1964)
- Kazuo Hiroike "Radial Distribution Function of Fluids I", Journal of the Physical Society of Japan 12 pp. 326-334 (1957)
- Kazuo Hiroike "Radial Distribution Function of Fluids II", Journal of the Physical Society of Japan 12 pp. pp. 864-873 (1957)
- J. G. Malherbe and W. Krauth "Selective-pivot sampling of radial distribution functions in asymmetric liquid mixtures", Molecular Physics 105 pp. 2393-2398 (2007)
- Sergey V. Sukhomlinov, Martin H. Müser "Determination of accurate, mean bond lengths from radial distribution functions", Journal of Chemical Physics 146 024506 (2017)














