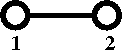Difference between revisions of "Mayer f-function"

Latest revision as of 18:50, 20 February 2015

The Mayer f-function, or f-bond is defined as (Ref. 1 Chapter 13 Eq. 13.2):

f_{12}=f({\mathbf r}_{12}) := \exp\left(-\frac{\Phi_{12}(r)}{k_BT}\right) -1

where

In other words, the Mayer function is the Boltzmann factor of the interaction potential, minus one.

Diagrammatically the Mayer f-function is written as

For the hard sphere model the Mayer f-function becomes:

f_{12}= \left\{ \begin{array}{lll} -1 & ; & r_{12} \leq \sigma ~~({\rm overlap})\\ 0 & ; & r_{12} > \sigma ~~({\rm no~overlap})\end{array} \right.

where $\sigma$ is the hard sphere diameter.

@@ Line 1: / Line 1: @@
-Definition:
+The '''Mayer ''f''-function''', or ''f-bond'' is defined as (Ref. 1 Chapter 13 Eq. 13.2):
-:<math>f_{ij}=f(r_{ij})= \exp\left(-\frac{u(r)}{k_BT}\right) -1 </math>
+:<math>f_{12}=f({\mathbf r}_{12}) := \exp\left(-\frac{\Phi_{12}(r)}{k_BT}\right) -1 </math>
 where
-* <math>k_B</math> is the [[Boltzmann constant]]
+* <math>k_B</math> is the [[Boltzmann constant]].
-* <math>T</math> is the temperature
+* <math>T</math> is the [[temperature]].
-* <math>u(r)</math> is the potential
+* <math>\Phi_{12}(r)</math> is the [[intermolecular pair potential]].
+In other words, the Mayer function is the [[Boltzmann factor]] of the interaction potential,
+minus one.
+[[Cluster diagrams | Diagrammatically]] the Mayer ''f''-function is written as
+:[[Image:Mayer_f_function.png]]
+==Hard sphere model==
+For the [[hard sphere model]]  the Mayer ''f''-function becomes:
+: <math>
+f_{12}= \left\{ \begin{array}{lll}
+-1 & ; & r_{12} \leq  \sigma ~~({\rm  overlap})\\
+      & ; & r_{12} > \sigma ~~({\rm  no~overlap})\end{array} \right.
+</math>
+where <math>\sigma</math> is the hard sphere diameter.
 ==References==
+# Joseph Edward Mayer and Maria Goeppert Mayer "Statistical Mechanics" John Wiley and Sons (1940)
+#[http://dx.doi.org/10.1063/1.1723631 Joseph E. Mayer "Contribution to Statistical Mechanics", Journal of Chemical Physics '''10''' pp. 629-643 (1942)]
 [[Category: Statistical mechanics]]
 [[Category: Integral equations]]