Hard sphere model

The hard sphere model (sometimes known as the rigid sphere model) is defined as
where is the intermolecular pair potential between two spheres at a distance , and is the diameter of the sphere. The hard sphere model can be considered to be a special case of the hard ellipsoid model, where each of the semi-axes has the same length, .
First simulations of hard spheres (1954-1957)
The hard sphere model, along with its two-dimensional manifestation hard disks, was one of the first ever systems studied using computer simulation techniques with a view to understanding the thermodynamics of the liquid and solid phases and their corresponding phase transition [1] [2] [3], much of this work undertaken at the Los Alamos Scientific Laboratory on the world's first electronic digital computer ENIAC [4].
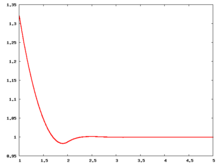
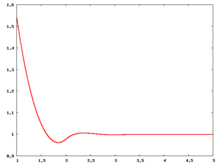
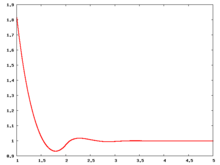
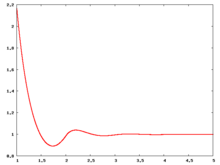
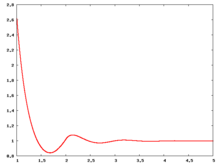
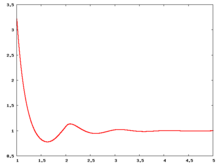
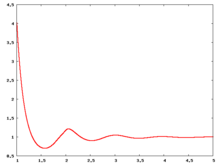
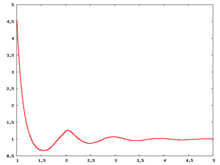
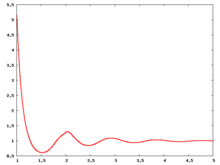
Liquid phase radial distribution function
The following are a series of plots of the hard sphere radial distribution function [5] shown for different values of the number density . The horizontal axis is in units of where is set to be 1. Click on image of interest to see a larger view.
The value of the radial distribution at contact, , can be used to calculate the pressure via the equation of state (Eq. 1 in [6])
where the second virial coefficient, , is given by
- .
Carnahan and Starling [7] provided the following expression for (Eq. 3 in [6])
where is the packing fraction.
Over the years many groups have studied the radial distribution function of the hard sphere model: [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18]
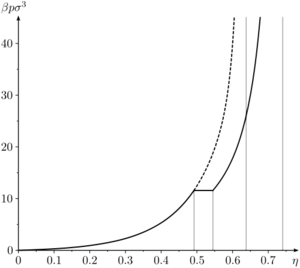
Liquid-solid transition
The hard sphere system undergoes a liquid-solid first order transition [19] [20], sometimes referred to as the Kirkwood-Alder transition [21]. The liquid-solid coexistence densities () has been calculated to be
Reference 1.041(4) 0.943(4) [19] 1.0376 0.9391 [22] 1.0367(10) 0.9387(10) [23] 1.0372 0.9387 [24] 1.0369(33) 0.9375(14) [25] 1.037 0.938 [26] 1.033(3) 0.935(2) [27] 1.03715(9) 0.93890(7) [28]
The coexistence pressure has been calculated to be
Reference 11.5727(10) [29] 11.57(10) [23] 11.567 [22] 11.55(11) [30] 11.54(4) [25] 11.50(9) [31] 11.48(11) [27] 11.43(17) [32] 11.550(4) [28]
The coexistence chemical potential has been calculated to be
The Helmholtz energy function (in units of ) is given by
Reference 4.887(3) 3.719(8) [27]
The melting and crystallization process has been studied by Isobe and Krauth [33].
Helmholtz energy function
Values for the Helmholtz energy function () are given in the following Table:
Reference 0.25 −1.766 0.002 Table I [34] 0.50 −0.152 0.002 Table I [34] 0.75 1.721 0.002 Table I [34] 1.04086 4.959 Table VI [24] 1.099975 5.631 Table VI [24] 1.150000 6.274 Table VI [24]
In [34] the free energies are given without the ideal gas contribution . Hence, it was added to the free energies in the table.
Interfacial Helmholtz energy function
The Helmholtz energy function of the solid–liquid interface has been calculated using the cleaving method giving (Ref. [35] Table I):
Solid structure
The Kepler conjecture states that the optimal packing for three dimensional spheres is either cubic or hexagonal close packing, both of which have maximum densities of [36] [37] [38]. However, for hard spheres at close packing the face centred cubic phase is the more stable [39], with a Helmholtz energy function difference in the thermodynamic limit between the hexagonal close packed and face centered cubic crystals at close packing of 0.001164(8) [40]. Recently evidence has been found for a metastable cI16 phase [41] indicating the "cI16 is a mechanically stable structure that can spontaneously emerge from a bcc starting point but it is thermodynamically metastable relative to fcc or hcp".
Direct correlation function
For the direct correlation function see: [42] [43]
Bridge function
Details of the bridge function for hard sphere can be found in the following publication [44]
Equations of state
- Main article: Equations of state for hard spheres
Virial coefficients
- Main article: Hard sphere: virial coefficients
Experimental results
Pusey and van Megen used a suspension of PMMA particles of radius 305 10 nm, suspended in poly-12-hydroxystearic acid [45] For results obtained from the Colloidal Disorder - Order Transition (CDOT) experiments performed on-board the Space Shuttles Columbia and Discovery see Ref. [46]
Mixtures
Related systems
Hard spheres in other dimensions:
- 1-dimensional case: hard rods.
- 2-dimensional case: hard disks.
- Hard hyperspheres
References
- ↑ Marshall N. Rosenbluth and Arianna W. Rosenbluth "Further Results on Monte Carlo Equations of State", Journal of Chemical Physics 22 pp. 881-884 (1954)
- ↑ W. W. Wood and J. D. Jacobson "Preliminary Results from a Recalculation of the Monte Carlo Equation of State of Hard Spheres", Journal of Chemical Physics 27 pp. 1207-1208 (1957)
- ↑ B. J. Alder and T. E. Wainwright "Phase Transition for a Hard Sphere System", Journal of Chemical Physics 27 pp. 1208-1209 (1957)
- ↑ The ENIAC Story
- ↑ The total correlation function data was produced using the computer code written by Jiří Kolafa
- ↑ 6.0 6.1 Fu-Ming Tao, Yuhua Song, and E. A. Mason "Derivative of the hard-sphere radial distribution function at contact", Physical Review A 46 pp. 8007-8008 (1992)
- ↑ N. F.Carnahan and K. E.Starling,"Equation of State for Nonattracting Rigid Spheres" Journal of Chemical Physics 51 pp. 635-636 (1969)
- ↑ John G. Kirkwood, Eugene K. Maun, and Berni J. Alder "Radial Distribution Functions and the Equation of State of a Fluid Composed of Rigid Spherical Molecules", Journal of Chemical Physics 18 pp. 1040- (1950)
- ↑ B. R. A. Nijboer and L. Van Hove "Radial Distribution Function of a Gas of Hard Spheres and the Superposition Approximation", Physical Review 85 pp. 777 - 783 (1952)
- ↑ B. J. Alder, S. P. Frankel, and V. A. Lewinson "Radial Distribution Function Calculated by the Monte-Carlo Method for a Hard Sphere Fluid", Journal of Chemical Physics 23 pp. 417- (1955)
- ↑ Francis H. Ree, R. Norris Keeler, and Shaun L. McCarthy "Radial Distribution Function of Hard Spheres", Journal of Chemical Physics 44 pp. 3407- (1966)
- ↑ W. R. Smith and D. Henderson "Analytical representation of the Percus-Yevick hard-sphere radial distribution function", Molecular Physics 19 pp. 411-415 (1970)
- ↑ J. A. Barker and D. Henderson "Monte Carlo values for the radial distribution function of a system of fluid hard spheres", Molecular Physics 21 pp. 187-191 (1971)
- ↑ J. M. Kincaid and J. J. Weis "Radial distribution function of a hard-sphere solid", Molecular Physics 34 pp. 931-938 (1977)
- ↑ S. Bravo Yuste and A. Santos "Radial distribution function for hard spheres", Physical Review A 43 pp. 5418-5423 (1991)
- ↑ Jaeeon Chang and Stanley I. Sandler "A real function representation for the structure of the hard-sphere fluid", Molecular Physics 81 pp. 735-744 (1994)
- ↑ Andrij Trokhymchuk, Ivo Nezbeda and Jan Jirsák "Hard-sphere radial distribution function again", Journal of Chemical Physics 123 024501 (2005)
- ↑ M. López de Haro, A. Santos and S. B. Yuste "On the radial distribution function of a hard-sphere fluid", Journal of Chemical Physics 124 236102 (2006)
- ↑ 19.0 19.1 William G. Hoover and Francis H. Ree "Melting Transition and Communal Entropy for Hard Spheres", Journal of Chemical Physics 49 pp. 3609-3617 (1968)
- ↑ Miguel Robles, Mariano López de Haro and Andrés Santos "Note: Equation of state and the freezing point in the hard-sphere model", Journal of Chemical Physics 140 136101 (2014)
- ↑ Alice P. Gast and William B. Russel "Simple Ordering in Complex Fluids", Physics Today 51 (12) pp. 24-30 (1998)
- ↑ 22.0 22.1 Daan Frenkel and Berend Smit "Understanding Molecular Simulation: From Algorithms to Applications", Second Edition (2002) (ISBN 0-12-267351-4) p. 261.
- ↑ 23.0 23.1 Andrea Fortini and Marjolein Dijkstra "Phase behaviour of hard spheres confined between parallel hard plates: manipulation of colloidal crystal structures by confinement", Journal of Physics: Condensed Matter 18 pp. L371-L378 (2006)
- ↑ 24.0 24.1 24.2 24.3 Carlos Vega and Eva G. Noya "Revisiting the Frenkel-Ladd method to compute the free energy of solids: The Einstein molecule approach", Journal of Chemical Physics 127 154113 (2007)
- ↑ 25.0 25.1 Eva G. Noya, Carlos Vega, and Enrique de Miguel "Determination of the melting point of hard spheres from direct coexistence simulation methods", Journal of Chemical Physics 128 154507 (2008)
- ↑ Ruslan L. Davidchack and Brian B. Laird "Simulation of the hard-sphere crystal–melt interface", Journal of Chemical Physics 108 pp. 9452-9462 (1998)
- ↑ 27.0 27.1 27.2 27.3 Enrique de Miguel "Estimating errors in free energy calculations from thermodynamic integration using fitted data", Journal of Chemical Physics 129 214112 (2008)
- ↑ 28.0 28.1 28.2 Craig Moir, Leo Lue, and Marcus N. Bannerman "Tethered-particle model: The calculation of free energies for hard-sphere systems", Journal of Chemical Physics 155 064504 (2021)
- ↑ 29.0 29.1 L. A. Fernández, V. Martín-Mayor, B. Seoane, and P. Verrocchio "Equilibrium Fluid-Solid Coexistence of Hard Spheres", Physical Review Letters 108 165701 (2012)
- ↑ Robin J. Speedy "Pressure of the metastable hard-sphere fluid", Journal of Physics: Condensed Matter 9 pp. 8591-8599 (1997)
- ↑ N. B. Wilding and A. D. Bruce "Freezing by Monte Carlo Phase Switch", Physical Review Letters 85 pp. 5138-5141 (2000)
- ↑ G. Odriozola "Replica exchange Monte Carlo applied to hard spheres", Journal of Chemical Physics 131 144107 (2009)
- ↑ Masaharu Isobe and Werner Krauth "Hard-sphere melting and crystallization with event-chain Monte Carlo", Journal of Chemical Physics 143 084509 (2015)
- ↑ 34.0 34.1 34.2 34.3 T. Schilling and F. Schmid "Computing absolute free energies of disordered structures by molecular simulation", Journal of Chemical Physics 131 231102 (2009)
- ↑ Ruslan L. Davidchack "Hard spheres revisited: Accurate calculation of the solid–liquid interfacial free energy", Journal of Chemical Physics 133 234701 (2010)
- ↑ Neil J. A. Sloane "Kepler's conjecture confirmed", Nature 395 pp. 435-436 (1998)
- ↑ Jacob Aron "Proof confirmed of 400-year-old fruit-stacking problem", New Scientist daily news 12 August (2014)
- ↑ C. F. Tejero, M. S. Ripoll, and A. Pérez "Pressure of the hard-sphere solid", Physical Review E 52 pp. 3632-3636 (1995)
- ↑ Leslie V. Woodcock "Computation of the free energy for alternative crystal structures of hard spheres", Faraday Discussions 106 pp. 325-338 (1997)
- ↑ Eva G. Noya and Noé G. Almarza "Entropy of hard spheres in the close-packing limit", Molecular Physics 113 pp. 1061-1068 (2015)
- ↑ Vadim B. Warshavsky, David M. Ford, and Peter A. Monson "On the mechanical stability of the body-centered cubic phase and the emergence of a metastable cI16 phase in classical hard sphere solids", Journal of Chemical Physics 148 024502 (2018)
- ↑ C. F. Tejero and M. López De Haro "Direct correlation function of the hard-sphere fluid", Molecular Physics 105 pp. 2999-3004 (2007)
- ↑ Matthew Dennison, Andrew J. Masters, David L. Cheung, and Michael P. Allen "Calculation of direct correlation function for hard particles using a virial expansion", Molecular Physics pp. 375-382 (2009)
- ↑ Jiri Kolafa, Stanislav Labik and Anatol Malijevsky "The bridge function of hard spheres by direct inversion of computer simulation data", Molecular Physics 100 pp. 2629-2640 (2002)
- ↑ P. N. Pusey and W. van Megen "Phase behaviour of concentrated suspensions of nearly hard colloidal spheres", Nature 320 pp. 340-342 (1986)
- ↑ Z. Chenga, P. M. Chaikina, W. B. Russelb, W. V. Meyerc, J. Zhub, R. B. Rogersc and R. H. Ottewilld, "Phase diagram of hard spheres", Materials & Design 22 pp. 529-534 (2001)
Related reading
- "Theory and Simulation of Hard-Sphere Fluids and Related Systems", Lecture Notes in Physics 753/2008 Springer (2008)
- Laura Filion, Michiel Hermes, Ran Ni and Marjolein Dijkstra "Crystal nucleation of hard spheres using molecular dynamics, umbrella sampling, and forward flux sampling: A comparison of simulation techniques", Journal of Chemical Physics 133 244115 (2010)
External links
- Hard disks and spheres computer code on SMAC-wiki.