Fused hard sphere chains: Difference between revisions
Jump to navigation
Jump to search
Carl McBride (talk | contribs) (Cleaned up the references section) |
|||
| Line 3: | Line 3: | ||
In the '''fused hard sphere chain''' model the ''molecule'' is built up form a string of overlapping [[hard sphere model|hard sphere sites]], each of diameter <math>\sigma</math>. | In the '''fused hard sphere chain''' model the ''molecule'' is built up form a string of overlapping [[hard sphere model|hard sphere sites]], each of diameter <math>\sigma</math>. | ||
An effective number of monomers can be applied to the fused hard sphere chain model by using the relarion (Ref. | An effective number of monomers can be applied to the fused hard sphere chain model by using the relarion (Ref. <ref>[http://dx.doi.org/10.1063/1.470528 Yaoqi Zhou, Carol K. Hall and George Stell "Thermodynamic perturbation theory for fused hard-sphere and hard-disk chain fluids", Journal of Chemical Physics '''103''' pp. 2688-2695 (1995)]</ref> Eq. 2.18) | ||
:<math>m_{\rm effective} = \frac{[1+(m-1)L^*]^3}{[1+(m-1)L^*(3-L^{*2})/2]^2}</math> | :<math>m_{\rm effective} = \frac{[1+(m-1)L^*]^3}{[1+(m-1)L^*(3-L^{*2})/2]^2}</math> | ||
where | where <math>m</math> is the number of monomer units in the model, and <math>L^*=L/\sigma</math> is the reduced bond length. | ||
The volume of the fused hard sphere chain is given by (Ref. | The volume of the fused hard sphere chain is given by (Ref. <ref name="BVD">[http://dx.doi.org/10.1063/1.459523 T. Boublík, C. Vega, and M. Diaz-Peña "Equation of state of chain molecules", Journal of Chemical Physics '''93''' pp. pp. 730-736 (1990)]</ref> Eq. 13) | ||
:<math>V_{\rm FHSC} =\frac{\pi \sigma^3}{6} \left( 1 + (m-1)\frac{3L^* - L^{*3}}{2} \right) ~~~~ | :<math>V_{\rm FHSC} =\frac{\pi \sigma^3}{6} \left( 1 + (m-1)\frac{3L^* - L^{*3}}{2} \right) ~~~~ | ||
| Line 18: | Line 18: | ||
</math> | </math> | ||
where <math>0<\gamma \leq \pi</math> is the minimal bond angle, and the surface area is given by (Ref. | where <math>0<\gamma \leq \pi</math> is the minimal bond angle, and the surface area is given by (Ref.<ref name="BVD" /> Eq. 12) | ||
:<math>S_{\mathrm FHSC} = \pi \sigma^2 \left( 1+\left( m-1 \right) L^* \right)</math> | :<math>S_{\mathrm FHSC} = \pi \sigma^2 \left( 1+\left( m-1 \right) L^* \right)</math> | ||
==Equation of state== | ==Equation of state== | ||
The Vörtler and Nezbeda [[Equations of state | equation of state]] is given by | The Vörtler and Nezbeda [[Equations of state | equation of state]] is given by <ref>[https://doi.org/10.1002/bbpc.19900940505 Horst L. Vörtler and I. Nezbeda "Volume-explicit equation of state and excess volume of mixing of fused hard sphere fluids", Berichte der Bunsen-Gesellschaft '''94''' pp. 559-563 (1990)]</ref> | ||
:<math>Z_{\mathrm{FHSC}}= 1+ (1+3\alpha)\eta_0(P^*) + C_{\rm FHSC}[\eta_0(P^*)]^{1.83}</math> | :<math>Z_{\mathrm{FHSC}}= 1+ (1+3\alpha)\eta_0(P^*) + C_{\rm FHSC}[\eta_0(P^*)]^{1.83}</math> | ||
| Line 34: | Line 34: | ||
:<math>\eta_0(P^*) = \frac{\sqrt{1+4(1+3\alpha)P^*}-1}{2+6\alpha}</math> | :<math>\eta_0(P^*) = \frac{\sqrt{1+4(1+3\alpha)P^*}-1}{2+6\alpha}</math> | ||
The Waziri and Hamad [[Equations of state | equation of state]] for fused hard sphere chain fluids is given by | The Waziri and Hamad [[Equations of state | equation of state]] for fused hard sphere chain fluids is given by <ref>[http://dx.doi.org/10.1021/ie800755s Saidu M. Waziri and Esam Z. Hamad "Volume-Explicit Equation of State for Fused Hard Sphere Chain Fluids", Industrial & Engineering Chemistry Research '''47''' pp. 9658-9662 (2008)]</ref> | ||
:<math>Z_{\mathrm{FHSC}} = 1 + 4m_{\mathrm{eff}}P^{*} + \frac{3}{4}m_{\mathrm{eff}}P^{*}\ln\left[\frac{3+P^{*}}{3+25P^{*}}\right] + \frac{216(m_{\mathrm{eff}} - 1)P^{*}}{(3+P^{*})(3+25P^{*})\{16+3\ln[(3+P^{*})/(3+25P^{*})]\}}</math> | :<math>Z_{\mathrm{FHSC}} = 1 + 4m_{\mathrm{eff}}P^{*} + \frac{3}{4}m_{\mathrm{eff}}P^{*}\ln\left[\frac{3+P^{*}}{3+25P^{*}}\right] + \frac{216(m_{\mathrm{eff}} - 1)P^{*}}{(3+P^{*})(3+25P^{*})\{16+3\ln[(3+P^{*})/(3+25P^{*})]\}}</math> | ||
| Line 41: | Line 41: | ||
:<math>m_{\mathrm{eff}}=\frac{2+3(m-1)L^{*}+2(m-1)^{2}L^{*2}+(m-1)L^{*3}}{2+3(m-1)L^{*}-(m-1)L^{*3}}</math> | :<math>m_{\mathrm{eff}}=\frac{2+3(m-1)L^{*}+2(m-1)^{2}L^{*2}+(m-1)L^{*3}}{2+3(m-1)L^{*}-(m-1)L^{*3}}</math> | ||
==See also== | ==See also== | ||
*[[Rigid fully flexible fused hard sphere model]] | *[[Rigid fully flexible fused hard sphere model]] | ||
==References== | ==References== | ||
<references/> | |||
;Related reading | |||
*[http://dx.doi.org/10.1080/00268979100100191 M. Whittle and A. J. Masters "Liquid crystal formation in a system of fused hard spheres", Molecular Physics '''72''' pp. 247-265 (1991)] | |||
*[http://dx.doi.org/10.1103/PhysRevE.64.011703 Carl McBride, Carlos Vega, and Luis G. MacDowell "Isotropic-nematic phase transition: Influence of intramolecular flexibility using a fused hard sphere model" Physical Review E '''64''' 011703 (2001)] | |||
*[http://dx.doi.org/10.1063/1.1517604 Carl McBride and Carlos Vega "A Monte Carlo study of the influence of molecular flexibility on the phase diagram of a fused hard sphere model", Journal of Chemical Physics '''117''' pp. 10370-10379 (2002)] | |||
*[http://dx.doi.org/10.1080/002689798168989 Antoine Chamoux and Aurelien Perera "On the linear hard sphere chain fluids", Molecular Physics '''93'' pp. 649-661 (1998)] | |||
[[category:liquid crystals]] | [[category:liquid crystals]] | ||
[[category:models]] | [[category:models]] | ||
Latest revision as of 20:45, 23 December 2018
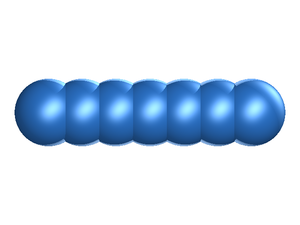
In the fused hard sphere chain model the molecule is built up form a string of overlapping hard sphere sites, each of diameter .
An effective number of monomers can be applied to the fused hard sphere chain model by using the relarion (Ref. [1] Eq. 2.18)
where is the number of monomer units in the model, and is the reduced bond length.
The volume of the fused hard sphere chain is given by (Ref. [2] Eq. 13)
where is the minimal bond angle, and the surface area is given by (Ref.[2] Eq. 12)
Equation of state[edit]
The Vörtler and Nezbeda equation of state is given by [3]
where
and
The Waziri and Hamad equation of state for fused hard sphere chain fluids is given by [4]
where
See also[edit]
References[edit]
- ↑ Yaoqi Zhou, Carol K. Hall and George Stell "Thermodynamic perturbation theory for fused hard-sphere and hard-disk chain fluids", Journal of Chemical Physics 103 pp. 2688-2695 (1995)
- ↑ 2.0 2.1 T. Boublík, C. Vega, and M. Diaz-Peña "Equation of state of chain molecules", Journal of Chemical Physics 93 pp. pp. 730-736 (1990)
- ↑ Horst L. Vörtler and I. Nezbeda "Volume-explicit equation of state and excess volume of mixing of fused hard sphere fluids", Berichte der Bunsen-Gesellschaft 94 pp. 559-563 (1990)
- ↑ Saidu M. Waziri and Esam Z. Hamad "Volume-Explicit Equation of State for Fused Hard Sphere Chain Fluids", Industrial & Engineering Chemistry Research 47 pp. 9658-9662 (2008)
- Related reading
- M. Whittle and A. J. Masters "Liquid crystal formation in a system of fused hard spheres", Molecular Physics 72 pp. 247-265 (1991)
- Carl McBride, Carlos Vega, and Luis G. MacDowell "Isotropic-nematic phase transition: Influence of intramolecular flexibility using a fused hard sphere model" Physical Review E 64 011703 (2001)
- Carl McBride and Carlos Vega "A Monte Carlo study of the influence of molecular flexibility on the phase diagram of a fused hard sphere model", Journal of Chemical Physics 117 pp. 10370-10379 (2002)
- Antoine Chamoux and Aurelien Perera "On the linear hard sphere chain fluids", Molecular Physics '93 pp. 649-661 (1998)

![{\displaystyle m_{\rm {effective}}={\frac {[1+(m-1)L^{*}]^{3}}{[1+(m-1)L^{*}(3-L^{*2})/2]^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/87c971dcd843e41062d341bfbcd501f4edea8001)





![{\displaystyle Z_{\mathrm {FHSC} }=1+(1+3\alpha )\eta _{0}(P^{*})+C_{\rm {FHSC}}[\eta _{0}(P^{*})]^{1.83}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/91afdc922fdfa04c21cdd02b43bebbdcfee850a4)
![{\displaystyle C_{\rm {FHSC}}=5.66\alpha (1-0.045[\alpha -1]^{1/2}\eta _{0})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4149ca3dad157caa5ae90ae3f5937fe4ef96457e)

![{\displaystyle Z_{\mathrm {FHSC} }=1+4m_{\mathrm {eff} }P^{*}+{\frac {3}{4}}m_{\mathrm {eff} }P^{*}\ln \left[{\frac {3+P^{*}}{3+25P^{*}}}\right]+{\frac {216(m_{\mathrm {eff} }-1)P^{*}}{(3+P^{*})(3+25P^{*})\{16+3\ln[(3+P^{*})/(3+25P^{*})]\}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/14883bcaf0a2995db20fbd4f59e80d64d62d9a07)
